
【題目】如圖,矩形OABC的邊OA、OC分別在x軸、y軸上,點B的坐標為(m,n)(m<0,
n>0),E點在邊BC上,F點在邊OA上.將矩形OABC沿EF折疊,點B正好與點O重合,雙曲線![]() 過點E.
過點E.
(1) 若m=-8,n =4,直接寫出E、F的坐標;
(2) 若直線EF的解析式為![]() ,求k的值;
,求k的值;
(3) 若雙曲線![]() 過EF的中點,直接寫出tan∠EFO的值.
過EF的中點,直接寫出tan∠EFO的值.

【答案】(1)E(-3,4)、F(-5,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1) 連接OE,BF,根據題意可知:![]() 設
設![]() 則
則![]() 根據勾股定理可得:
根據勾股定理可得:![]() 即
即![]() 解得:
解得:![]() 即可求出點E的坐標,同理求出點F的坐標.
即可求出點E的坐標,同理求出點F的坐標.
(2) 連接BF、OE,連接BO交EF于G由翻折可知:GO=GB,BE=OE,證明△BGE≌△OGF,證明四邊形OEBF為菱形,令y=0,則![]() ,解得
,解得![]() , 根據菱形的性質得OF=OE=BE=BF=
, 根據菱形的性質得OF=OE=BE=BF=![]() 令y=n,則
令y=n,則![]() ,解得
,解得![]() 則CE=
則CE=![]() ,在Rt△COE中, 根據勾股定理列出方程
,在Rt△COE中, 根據勾股定理列出方程![]() ,即可求出點E的坐標,即可求出k的值;
,即可求出點E的坐標,即可求出k的值;
(3) 設EB=EO=x,則CE=-m-x,在Rt△COE中,根據勾股定理得到(-m-x)2+n2=x2,解得![]() ,求出點E(
,求出點E(![]() )、F(
)、F(![]() ),根據中點公式得到EF的中點為(
),根據中點公式得到EF的中點為(![]() ),將E(
),將E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得![]() ,得m2=2n2
,得m2=2n2
即可求出tan∠EFO=![]() .
.
解:(1)如圖:連接OE,BF,

E(-3,4)、F(-5,0)
(2) 連接BF、OE,連接BO交EF于G由翻折可知:GO=GB,BE=OE

可證:△BGE≌△OGF(ASA)
∴BE=OF
∴四邊形OEBF為菱形
令y=0,則![]() ,解得
,解得![]() ,∴OF=OE=BE=BF=
,∴OF=OE=BE=BF=![]()
令y=n,則![]() ,解得
,解得![]() ∴CE=
∴CE=![]()
在Rt△COE中,![]() ,
,
解得![]()
∴E(![]() )
)
∴![]()
(3) 設EB=EO=x,則CE=-m-x,
在Rt△COE中,(-m-x)2+n2=x2,解得![]()
∴E(![]() )、F(
)、F(![]() )
)
∴EF的中點為(![]() )
)
將E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得
![]() ,得m2=2n2
,得m2=2n2
∴tan∠EFO=![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
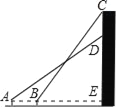
【題目】如圖所示,小王在校園上的A處正面觀測一座教學樓墻上的大型標牌,測得標牌下端D處的仰角為30°,然后他正對大樓方向前進5m到達B處,又測得該標牌上端C處的仰角為45°.若該樓高為16.65m,小王的眼睛離地面1.65m,大型標牌的上端與樓房的頂端平齊.求此標牌上端與下端之間的距離(![]() ≈1.732,結果精確到0.1m).
≈1.732,結果精確到0.1m).
查看答案和解析>>
科目:初中數學 來源: 題型:
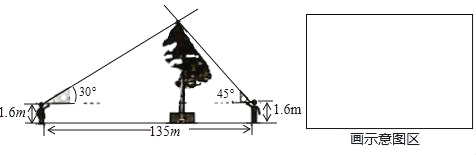
【題目】清明節假期,小紅和小陽隨爸媽去旅游,他們在景點看到一棵古松樹,小紅驚訝的說:“呀!這棵樹真高!有60多米.”小陽卻不以為然:“60多米?我看沒有.”兩個人爭論不休,爸爸笑著說:“別爭了,正好我帶了一副三角板,用你們學過的知識量一量、算一算,看誰說的對吧!”
小紅和小陽進行了以下測量:如圖所示,小紅和小陽分別在樹的東西兩側同一地平線上,他們用手平托三角板,保持三角板的一條直角邊與地平面平行,然后前后移動各自位置,使目光沿著三角板的斜邊正好經過樹的最高點,這時,測得小紅和小陽之間的距離為135米,他們的眼睛到地面的距離都是1.6米.
(1)請在指定區域內畫出小紅和小陽測量古松樹高的示意圖;
(2)通過計算說明小紅和小陽誰的說法正確(計算結果精確到0.1)(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中數學 來源: 題型:
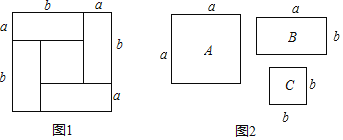
【題目】利用圖形面積可以解釋代數恒等式的正確性,如圖1可以驗證一個代數恒等式(a+b)2=(a﹣b)2+4ab.
(1)如圖2,用若干張A,B,C的卡片拼成一個長方形面積為(2a+b)(a+b),那么需要A,B,C卡片各多少張?
(2)如果用1張A,5張B,6張C拼成一個長方形,那么這個長方形的邊長分別是 和 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有A、B兩種手機上網計費方式,收費標準如下表所示:
計費方式 | 月使用費/元 | 包月上網時間/分 | 超時費/(元/分) |
A | 30 | 120 | 0.20 |
B | 60 | 320 | 0.25 |
設上網時間為x分鐘,
(1)若按方式A和方式B的收費金額相等,求x的值;
(2)若上網時間x超過320分鐘,選擇哪一種方式更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,AB = 6cm,AD=10 cm,點P在AD 邊上以每秒1 cm的速度從點A向點D運動,點Q在BC邊上,以每秒4 cm的速度從點C出發,在CB間往返運動,兩個點同時出發,當點P到達點D時停止 (同時點Q也停止),在運動以后,以P、D、Q、B四點組成平行四邊形的次數有( )
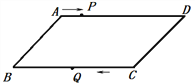
A. 1 次 B. 2次 C. 3次 D. 4次
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料1:
對于兩個正實數![]() ,由于
,由于![]() ,所以
,所以![]() ,即
,即![]() ,所以得到
,所以得到![]() ,并且當
,并且當![]() 時,
時,![]()
閱讀材料2:
若![]() ,則
,則![]() ,因為
,因為![]() ,
,![]() ,所以由閱讀材料1可得:
,所以由閱讀材料1可得:![]() ,即
,即![]() 的最小值是2,只有
的最小值是2,只有![]() 時,即
時,即![]() =1時取得最小值.
=1時取得最小值.
根據以上閱讀材料,請回答以下問題:
(1)比較大小
![]()
![]() (其中
(其中![]() ≥1);
≥1); ![]() -2(其中
-2(其中![]() <-1)
<-1)
(2)已知代數式![]() 變形為
變形為![]() ,求常數
,求常數![]() 的值
的值
(3)當![]() = 時,
= 時,![]() 有最小值,最小值為 (直接寫出答案).
有最小值,最小值為 (直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
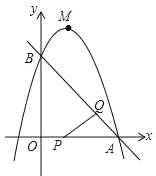
【題目】如圖,已知直線y=﹣x+3與x軸、y軸分別交于A,B兩點,拋物線y=﹣x2+bx+c經過A,B兩點,點P在線段OA上,從點A以1個單位/秒的速度勻速運動;同時,點Q在線段AB上,從點A出發,向點B以![]() 個單位/秒的速度勻速運動,連接PQ,設運動時間為t秒.
個單位/秒的速度勻速運動,連接PQ,設運動時間為t秒.
(1)求拋物線的解析式;
(2)當t為何值時,△APQ為直角三角形;
(3)過點P作PE∥y軸,交AB于點E,過點Q作QF∥y軸,交拋物線于點F,連接EF,當EF∥PQ時,求點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
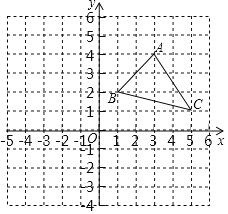
【題目】△ABC在平面直角坐標系中的位置如圖所示:
(1)寫出點A,B,C三點的坐標;
(2)若△ABC各頂點的橫坐標不變,縱坐標都乘以﹣1,請你在同一坐標系中描出對應的點A',B',C',并依次連接這三點,所得的△A'B'C'與原△ABC的位置關系是什么?
(3)在x軸上作出一點P,使得AP平分∠BAC.(保留作圖痕跡,不寫作法)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com