
【題目】在邊長(zhǎng)為1個(gè)單位長(zhǎng)度的正方形網(wǎng)格中建立如圖所示的平面直角坐標(biāo)系,![]() 的頂點(diǎn)都在格點(diǎn)上
的頂點(diǎn)都在格點(diǎn)上![]() 小正方形的頂點(diǎn)稱為格點(diǎn)
小正方形的頂點(diǎn)稱為格點(diǎn)![]() ,請(qǐng)解答下列問題:
,請(qǐng)解答下列問題:
![]() 作出
作出![]() 關(guān)于y軸對(duì)稱的
關(guān)于y軸對(duì)稱的![]() ,點(diǎn)
,點(diǎn)![]() 與A、
與A、![]() 與B對(duì)應(yīng),并回答下列兩個(gè)問題:
與B對(duì)應(yīng),并回答下列兩個(gè)問題:
![]() 寫出點(diǎn)
寫出點(diǎn)![]() 的坐標(biāo):
的坐標(biāo):![]() 已知點(diǎn)P是線段
已知點(diǎn)P是線段![]() 上任意一點(diǎn),用恰當(dāng)?shù)姆绞奖硎军c(diǎn)P的坐標(biāo).
上任意一點(diǎn),用恰當(dāng)?shù)姆绞奖硎军c(diǎn)P的坐標(biāo).
![]() 若
若![]() 平移后得
平移后得![]() ,A的對(duì)應(yīng)點(diǎn)
,A的對(duì)應(yīng)點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,寫出點(diǎn)B的對(duì)應(yīng)點(diǎn)
,寫出點(diǎn)B的對(duì)應(yīng)點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).

【答案】(1)![]() ;
;![]() P
P![]() ;
;![]() .
.
【解析】
(1)根據(jù)點(diǎn)坐標(biāo)關(guān)于y軸對(duì)稱的特征,找到![]() 三個(gè)頂點(diǎn)的對(duì)稱點(diǎn),順次連接即可得到關(guān)于y軸對(duì)稱的三角形;線段AA1上點(diǎn)的縱坐標(biāo)都是4,-2≤橫坐標(biāo)≤2,據(jù)此可求解;
三個(gè)頂點(diǎn)的對(duì)稱點(diǎn),順次連接即可得到關(guān)于y軸對(duì)稱的三角形;線段AA1上點(diǎn)的縱坐標(biāo)都是4,-2≤橫坐標(biāo)≤2,據(jù)此可求解;
(2)根據(jù)A(2,4),A2(-1,-1)可知平移的方向和距離,從而求出B2的坐標(biāo).
解:![]() 如圖所示:
如圖所示:
![]() 圖
圖![]() 的坐標(biāo)
的坐標(biāo)![]() ;
;![]() 點(diǎn)P的坐標(biāo)
點(diǎn)P的坐標(biāo)![]() ;
;![]() 點(diǎn)A(2,4)平移后坐標(biāo)為A2(-1,-1),
點(diǎn)A(2,4)平移后坐標(biāo)為A2(-1,-1),
由-1-2=-3,-1-4=-5,可知△ABC向左平移3個(gè)單位長(zhǎng)度,向下平移5個(gè)單位長(zhǎng)度,
∴點(diǎn)![]() 的坐標(biāo)
的坐標(biāo)![]() .
.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
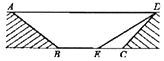
【題目】為緩解交通擁堵,某區(qū)擬計(jì)劃修建一地下通道,該通道一部分的截面如圖所示(圖中地面 ![]() 與通道
與通道 ![]() 平行),通道水平寬度
平行),通道水平寬度 ![]() 為8米,
為8米, ![]() ,通道斜面
,通道斜面 ![]() 的長(zhǎng)為6米,通道斜面
的長(zhǎng)為6米,通道斜面 ![]() 的坡度
的坡度 ![]() .
.
(1)求通道斜面 ![]() 的長(zhǎng)為米;
的長(zhǎng)為米;
(2)為增加市民行走的舒適度,擬將設(shè)計(jì)圖中的通道斜面 ![]() 的坡度變緩,修改后的通道斜面
的坡度變緩,修改后的通道斜面 ![]() 的坡角為30°,求此時(shí)
的坡角為30°,求此時(shí) ![]() 的長(zhǎng).(結(jié)果保留根號(hào))
的長(zhǎng).(結(jié)果保留根號(hào))
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形ABCD中,E是AD邊的中點(diǎn),BE⊥AC,垂足為點(diǎn)F,連接DF,分析下列四個(gè)結(jié)論:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= ![]() .
.
其中正確的結(jié)論有( )
A.4個(gè)
B.3個(gè)
C.2個(gè)
D.1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,銳角![]() 中,
中,![]() ,若想找一點(diǎn)P,使得
,若想找一點(diǎn)P,使得![]() 與
與![]() 互補(bǔ),甲、乙、丙三人作法分別如下:
互補(bǔ),甲、乙、丙三人作法分別如下:
甲:以B為圓心,AB長(zhǎng)為半徑畫弧交AC于P點(diǎn),則P即為所求;
乙:分別以B,C為圓心,AB,AC長(zhǎng)為半徑畫弧交于P點(diǎn),則P即為所求;
丙:作BC的垂直平分線和![]() 的平分線,兩線交于P點(diǎn),則P即為所求.
的平分線,兩線交于P點(diǎn),則P即為所求.
對(duì)于甲、乙、丙三人的作法,下列敘述正確的是![]()
![]()

A. 三人皆正確B. 甲、丙正確,乙錯(cuò)誤
C. 甲正確,乙、丙錯(cuò)誤D. 甲錯(cuò)誤,乙、丙正確
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】星期日早晨,小青從家出發(fā)勻速去森林公園溜冰,小青出發(fā)一段時(shí)間后,他媽媽發(fā)現(xiàn)小青忘帶了溜冰鞋,于是立即騎自行車沿小青行進(jìn)的路線勻速去追趕,媽媽追上小青后,立即沿原路線勻速返回家,但由于路上行人漸多,媽媽返回時(shí)騎車的速度只是原來速度的三分之二,小青繼續(xù)以原速度步行前往森林公園,媽媽與小青之間的路程![]() 米
米![]() 與小青從家出發(fā)后步行的時(shí)間
與小青從家出發(fā)后步行的時(shí)間![]() 分
分![]() 之間的關(guān)系如圖所示,當(dāng)媽媽剛回到家時(shí),小青到森林公園的路程還有______米
之間的關(guān)系如圖所示,當(dāng)媽媽剛回到家時(shí),小青到森林公園的路程還有______米![]()

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知點(diǎn)E、F在直線AB上,點(diǎn)G在線段CD上,ED與FG交于點(diǎn)H,∠C=∠EFG,∠CED=∠GHD.
(1)求證:CE∥GF;
(2)試判斷∠AED與∠D之間的數(shù)量關(guān)系,并說明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,一只電子狗從原點(diǎn)O出發(fā),按向上→向右→向下→向下→向右的方向依次不斷移動(dòng),每次移動(dòng)1個(gè)單位長(zhǎng)度,其行走路線如圖所示,則A3020的坐標(biāo)為( )

A.(1007,1)B.(1007,﹣1)C.(504,1)D.(504,﹣1)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖1,△ACB和△DCE均為等邊三角形,點(diǎn)A,D,E在同一直線上,連接BE,則∠AEB的度數(shù)為__________.
(2)如圖2,△ACB和△DCE均為等腰直角三角形,∠ACB=∠DCE=90°,點(diǎn)A,D,E在同一直線上,CM為△DCE中DE邊上的高,連接BE.求∠AEB的度數(shù)及線段CM,AE,BE之間的數(shù)量關(guān)系,并說明理由.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com