
【題目】某部隊凌晨5∶00乘車從駐地勻速趕往離駐地90千米的B處執行任務,出發20分鐘后在途中遇到提前出發的先遣分隊.部隊6∶00到達B處后,空車原速返回接應先遣分隊于6∶40準時到達B處.已知汽車和先遣分隊距離B處的距離y(km)與汽車行駛時間t(h)的函數關系圖象如圖14所示.
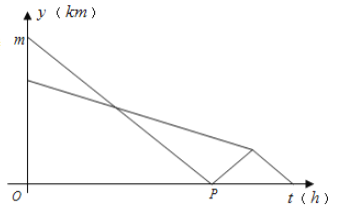
(1) 圖中m=___________,P點坐標為___________;
(2) 求汽車第一次行駛到B地時,汽車行駛路程y(km)與行駛時間t(h)的函數關系式;
(3) 求先遣分隊的步行速度;
(4) 先遣分隊比大部隊早出發多少小時?
【答案】(1)90,(1,0);(2) y汽車=![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根據題意可以得到點m的值和點P的坐標,本題得以解決;
(2)根據題意可以得到各段對應的函數解析式,從而可以解答本題;
(3)根據題意可以得到先遣分隊在相應的時間內所走的路程,從而可以得到先遣分隊的步行速度;
(4)由題意可得到先遣分隊先出發的路程,從而可以先遣分隊比大部隊早出發多少小時.
解:(1)由題意可得,
圖中m的值是90,點P的坐標是(1,0),
故答案為:90,(1,0);
(2) 當0≤t≤1時,設y=kt+b,
則![]()
解得,![]() ,
,
即當0≤t≤1時,y=-90t+90;
(3) 由題意可得,
先遣分隊的步行速度為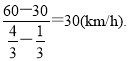
即先遣分隊的速度是30km/h;
(4) 當0<t≤![]() 時,y先遣分隊=-30t + 70,
時,y先遣分隊=-30t + 70,
令t=0,則y先遣分隊=70.
先遣分隊比大部隊早出發的時間為(90-70)÷30=![]() (h)
(h)


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
【題目】由于霧霾天氣頻發,市場上防護口罩出現熱銷,某醫藥公司每月固定生產甲、乙兩種型號的防霧霾口罩共20萬只,且所有產品當月全部售出,原料成本、銷售單價及工人生產提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
銷售單價 | 18 | 12 |
生產提成 | 1 | 0.8 |
(1)若該公司五月份的銷售收入為300萬元,求甲、乙兩種型號的產品分別是多少萬只?
(2)公司實行計件工資制,即工人每生產一只口罩獲得一定金額的提成,如果公司六月份投入總成本(原料總成本+生產提成總額)不超過239萬元,應怎樣安排甲、乙兩種型號的產量,可使該月公司所獲利潤最大?并求出最大利潤(利潤=銷售收入﹣投入總成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝超市購進單價為30元的童裝若干件,物價部門規定其銷售單價不低于每件30元,不高于每件60元.銷售一段時間后發現:當銷售單價為60元時,平均每月銷售量為80件,而當銷售單價每降低10元時,平均每月能多售出20件.同時,在銷售過程中,每月還要支付其他費用450元.設銷售單價為x元,平均月銷售量為y件.
(1)求出y與x的函數關系式,并寫出自變量x的取值范圍.
(2)當銷售單價為多少元時,銷售這種童裝每月可獲利1800元?
(3)當銷售單價為多少元時,銷售這種童裝每月獲得利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,將兩個完全相同的三角形紙片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
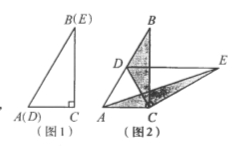


(1)操作發現如圖2,固定△ABC,使△DEC繞點C旋轉。當點D恰好落在BC邊上時,填空:線段DE與AC的位置關系是 ;
② 設△BDC的面積為S1,△AEC的面積為S2。則S1與S2的數量關系是 。
(2)猜想論證
當△DEC繞點C旋轉到圖3所示的位置時,小明猜想(1)中S1與S2的數量關系仍然成立,并嘗試分別作出了△BDC和△AEC中BC,CE邊上的高,請你證明小明的猜想。
(3)拓展探究
已知∠ABC=600,點D是其角平分線上一點,BD=CD=4,OE∥AB交BC于點E(如圖4),若在射線BA上存在點F,使S△DCF =S△BDC,請直接寫出相應的BF的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某年5月,我國南方某省A、B兩市遭受嚴重洪澇災害,1.5萬人被迫轉移,鄰近縣市C、D獲知A、B兩市分別急需救災物資200噸和300噸的消息后,決定調運物資支援災區.已知C市有救災物資240噸,D市有救災物資260噸,現將這些救災物資全部調往A、B兩市.已知從C市運往A、B兩市的費用分別為每噸20元和25元,從D市運往往A、B兩市的費用別為每噸15元和30元,設從D市運往B市的救災物資為x噸.
(1)請填寫下表
A(噸) | B(噸) | 合計(噸) | |
C |
|
| 240 |
D |
| x | 260 |
總計(噸) | 200 | 300 | 500 |
(2)設C、D兩市的總運費為w元,求w與x之間的函數關系式,并寫出自變量x的取值范圍;
(3)經過搶修,從D市到B市的路況得到了改善,縮短了運輸時間,運費每噸減少m元(m>0),其余路線運費不變.若C、D兩市的總運費的最小值不小于10320元,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
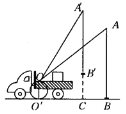
【題目】小劉同學在課外活動中觀察吊車的工作過程,繪制了如圖所示的平面圖形.已知吊車吊臂的支點O距離地面的高度OO′=2米.當吊臂頂端由A點抬升至 A′點(吊臂長度不變)時,地面B處的重物(大小忽略不計)被吊至B′處,緊繃著的吊繩A′B′=AB.AB垂直地面 O′B于點B,A′B′垂直地面O′B于點C,吊臂長度OA′=OA=10米,且cosA![]() ,sinA′
,sinA′![]() .求此重物在水平方向移動的距離BC.
.求此重物在水平方向移動的距離BC.
查看答案和解析>>
科目:初中數學 來源: 題型:
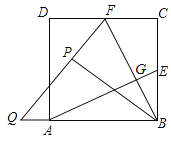
【題目】如圖,在邊長為2的正方形ABCD中,E,F分別為BC、CD的中點,連接AE,BF交于點G,將△BCF沿BF對折,得到△BPF,延長FP交BA延長線于點Q,下列結論正確都有( )個.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四邊形ECFG=2S△BGE
;④S四邊形ECFG=2S△BGE
A.5B.4C.3D.2
查看答案和解析>>
科目:初中數學 來源: 題型:
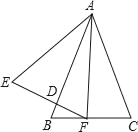
【題目】如圖,△ABC與△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.給出下列結論:①∠AFC=∠C;②DF=BF;③△ADE∽△FDB;④∠BFD=∠CAF.其中正確的結論是_____(填寫所有正確結論的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
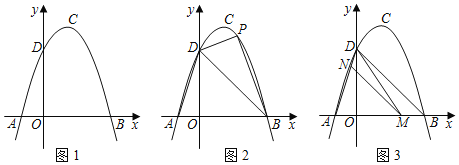
【題目】如圖1,拋物線y=﹣x2+bx+c(a≠0)的頂點為C,交x軸于A![]() 、B
、B![]() 兩點,交y軸于點D.
兩點,交y軸于點D.
(1)求拋物線的解析式;并直接寫出點C的坐標.
(2)如圖2,點P為直線BD上方拋物線上一點,作PE⊥BD于點E,AF⊥BD于點F若![]() ,請求出點P的坐標.
,請求出點P的坐標.
(3)如圖3,M為線段AB上的一點,過點M作MN∥BD,交線段AD于點N,連接MD,若△DNM∽△BMD,請求出點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com