
某公司銷售一種新型節(jié)能電子小產(chǎn)品,現(xiàn)準(zhǔn)備從國內(nèi)和國外兩種銷售方案中選擇一種進行銷售:①若只在國內(nèi)銷售,銷售價格y(元/件)與月銷量x(件)的函數(shù)關(guān)系式為y=- x+150,成本為20元/件,月利潤為W內(nèi)(元);②若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數(shù),10≤a≤40),當(dāng)月銷量為x(件)時,每月還需繳納
x+150,成本為20元/件,月利潤為W內(nèi)(元);②若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數(shù),10≤a≤40),當(dāng)月銷量為x(件)時,每月還需繳納 x2元的附加費,月利潤為W外(元).
x2元的附加費,月利潤為W外(元).
(1)若只在國內(nèi)銷售,當(dāng)x=1000(件)時,y= (元/件);
(2)分別求出W內(nèi)、W外與x間的函數(shù)關(guān)系式(不必寫x的取值范圍);
(3)若在國外銷售月利潤的最大值與在國內(nèi)銷售月利潤的最大值相同,求a的值.
(1)140;(2)W內(nèi)=- x2+130x,W外=-
x2+130x,W外=- x2+ (150-a)x;(3)a=20.
x2+ (150-a)x;(3)a=20.
解析試題分析:(1)將x=1000代入函數(shù)關(guān)系式求得y,;
(2)根據(jù)等量關(guān)系“利潤=銷售額﹣成本”“利潤=銷售額﹣成本﹣附加費”列出函數(shù)關(guān)系式;
(3)對w內(nèi)函數(shù)的函數(shù)關(guān)系式求得最大值,再求出w外的最大值并令二者相等求得a值.
試題解析:(1)x=1000,y=- ×1000+150=140;
×1000+150=140;
(2)W內(nèi)=(y-20)x=(- x+150-20)x=-
x+150-20)x=- x2+130x.
x2+130x.
W外=(150-a)x- x2=-
x2=- x2+(150-a)x;
x2+(150-a)x;
(3)W內(nèi)=- x2+130x=-
x2+130x=- (x-6500)2+422500,
(x-6500)2+422500,
由W外=- x2+(150-a)x得:W外最大值為:(750-5a)2,
x2+(150-a)x得:W外最大值為:(750-5a)2,
所以:(750-5a)2=422500.
解得a=280或a=20.
經(jīng)檢驗,a=280不合題意,舍去,
∴a=20.
考點:二次函數(shù)的應(yīng)用.


 小學(xué)課堂作業(yè)系列答案
小學(xué)課堂作業(yè)系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,直角坐標(biāo)系中Rt△ABO,其頂點為A(0, 1)、B(2, 0)、O(0, 0),將此三角板繞原點O逆時針旋轉(zhuǎn)90°,得到Rt△A′B′O.
(1)一拋物線經(jīng)過點A′、B′、B,求該拋物線的解析式;
(2)設(shè)點P是在第一象限內(nèi)拋物線上的一動點,是否存在點P,使四邊形PB′A′B的面積是△A′B′O面積4倍?若存在,請求出P的坐標(biāo);若不存在,請說明理由.
(3)在(2)的條件下,試指出四邊形PB′A′B是哪種形狀的四邊形?并寫出四邊形PB′A′B的兩條性質(zhì).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
在平面直角坐標(biāo)系 中,矩形OABC過原點O,且A(0,2)、C(6,0),∠AOC的平分線交AB于點D.
中,矩形OABC過原點O,且A(0,2)、C(6,0),∠AOC的平分線交AB于點D.
(1)直接寫出點B的坐標(biāo);
(2)如圖,點P從點O出發(fā),以每秒 個單位長度的速度沿射線OD方向移動;同時點Q從點O出發(fā),以每秒2個單位長度的速度沿
個單位長度的速度沿射線OD方向移動;同時點Q從點O出發(fā),以每秒2個單位長度的速度沿 軸正方向移動.設(shè)移動時間為
軸正方向移動.設(shè)移動時間為 秒.
秒.
①當(dāng)t為何值時,△OPQ的面積等于1;
②當(dāng)t為何值時,△PQB為直角三角形;
(3)已知過O、P、Q三點的拋物線解析式為y=- (x-t)2+t(t>0).問是否存在某一時刻t,將△PQB繞某點旋轉(zhuǎn)180°后,三個對應(yīng)頂點恰好都落在上述拋物線上?若存在,求出t的值;若不存在,請說明理由.
(x-t)2+t(t>0).問是否存在某一時刻t,將△PQB繞某點旋轉(zhuǎn)180°后,三個對應(yīng)頂點恰好都落在上述拋物線上?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
某商人如果將進貨價為8元的商品按每件10元出售,每天可銷售100件,現(xiàn)采用提高售出價,減少進貨量的辦法增加利潤,已知這種商品每漲價1元其銷售量就要減少10件,問他將售出價x定為多少元時,才能使每天所賺的利潤y 最大?并求出最大利潤。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
動物園計劃用長為120米的鐵絲圍成如圖所示的兔籠,(不包括頂棚)供學(xué)習(xí)小組的同學(xué)參觀,其中一面靠墻,(墻足夠長)怎樣設(shè)計圍成的面積最大?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,在平面直角坐標(biāo)系中,頂點為(4,1)的拋物線交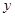 軸于點
軸于點 ,交
,交 軸于
軸于 ,
, 兩點(點
兩點(點 在點
在點 的左側(cè)),已知
的左側(cè)),已知 點坐標(biāo)為(6,0).
點坐標(biāo)為(6,0).
(1)求此拋物線的解析式;
(2)聯(lián)結(jié)AB,過點 作線段
作線段 的垂線交拋物線于點
的垂線交拋物線于點 ,如果以點
,如果以點 為圓心的圓與拋物線的對稱軸
為圓心的圓與拋物線的對稱軸 相切,先補全圖形,再判斷直線
相切,先補全圖形,再判斷直線 與⊙
與⊙ 的位置關(guān)系并加以證明;
的位置關(guān)系并加以證明;
(3)已知點 是拋物線上的一個動點,且位于
是拋物線上的一個動點,且位于 ,
, 兩點之間.問:當(dāng)點
兩點之間.問:當(dāng)點 運動到什么位置時,
運動到什么位置時, 的面積最大?求出
的面積最大?求出 的最大面積.
的最大面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知直線 分別與y軸、x軸相交于A、B兩點,與二次函數(shù)
分別與y軸、x軸相交于A、B兩點,與二次函數(shù) 的圖像交于A、C兩點.
的圖像交于A、C兩點.
(1)當(dāng)點C坐標(biāo)為( ,
,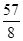 )時,求直線AB的解析式;
)時,求直線AB的解析式;
(2)在(1)中,如圖,將△ABO沿y軸翻折180°,若點B的對應(yīng)點D恰好落在二次函數(shù) 的圖像上,求點D到直線AB的距離;
的圖像上,求點D到直線AB的距離;
(3)當(dāng)-1≤x≤1時,二次函數(shù) 有最小值-3,求實數(shù)m的值.
有最小值-3,求實數(shù)m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知拋物線 (m是常數(shù),
(m是常數(shù),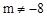 )與x軸有兩個不同的交點A、B,點A、點B關(guān)于直線x=1對稱,拋物線的頂點為C.
)與x軸有兩個不同的交點A、B,點A、點B關(guān)于直線x=1對稱,拋物線的頂點為C.
(1)此拋物線的解析式;
(2)求點A、B、C的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖所示,在平面直角坐標(biāo)系中,Rt△OBC的兩條直角邊分別落在x軸、y軸上,且OB=1,OC=3,將△OBC繞原點O順時針旋轉(zhuǎn)90°得到△OAE,將△OBC沿y軸翻折得到△ODC,AE與CD交于點F.
(1)若拋物線過點A、B、C, 求此拋物線的解析式;
(2)求△OAE與△ODC重疊的部分四邊形ODFE的面積;
(3)點M是第三象限內(nèi)拋物線上的一動點,點M在何處時△AMC的面積最大?最大面積是多少?求出此時點 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com