
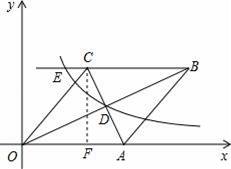
如圖,已知:如圖,在直角坐標系中,有菱形OABC,A點的坐標為(10,0),對角線OB、AC相交于D點,雙曲線y=
 (x>0)經過D點,交BC的延長線于E點,且OB•AC=160,有下列四個結論:
(x>0)經過D點,交BC的延長線于E點,且OB•AC=160,有下列四個結論:
①雙曲線的解析式為y=
 (x>0);②E點的坐標是(5,8);③sin∠COA=
(x>0);②E點的坐標是(5,8);③sin∠COA=
 ;④AC+OB=12
;④AC+OB=12
 .其中正確的結論有( )
.其中正確的結論有( )


A.1個 B.2個 C.3個 D.4個
B【考點】反比例函數綜合題.
【分析】過點C作CF⊥x軸于點F,由OB•AC=160可求出菱形的面積,由A點的坐標為(10,0)可求出CF的長,由勾股定理可求出OF的長,故可得出C點坐標,對角線OB、AC相交于D點可求出D點坐標,用待定系數法可求出雙曲線y=
 (x>0)的解析式,由反比例函數的解析式與直線BC的解析式聯立即可求出E點坐標;由sin∠COA=
(x>0)的解析式,由反比例函數的解析式與直線BC的解析式聯立即可求出E點坐標;由sin∠COA=
 可求出∠COA的正弦值;根據A、C兩點的坐標可求出AC的長,由OB•AC=160即可求出OB的長.
可求出∠COA的正弦值;根據A、C兩點的坐標可求出AC的長,由OB•AC=160即可求出OB的長.
【解答】解:過點C作CF⊥x軸于點F,
∵OB•AC=160,A點的坐標為(10,0),
∴OA•CF=
 OB•AC=
OB•AC=
 ×160=80,菱形OABC的邊長為10,
×160=80,菱形OABC的邊長為10,
∴CF=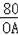
 =
=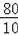
 =8,
=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=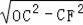
 =
=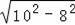
 =6,
=6,
∴C(6,8),
∵點D時線段AC的中點,
∴D點坐標為(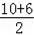
 ,
,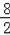
 ),即(8,4),
),即(8,4),
∵雙曲線y=
 (x>0)經過D點,
(x>0)經過D點,
∴4=
 ,即k=32,
,即k=32,
∴雙曲線的解析式為:y=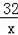
 (x>0),故①錯誤;
(x>0),故①錯誤;
∵CF=8,
∴直線CB的解析式為y=8,
∴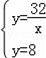
 ,解得x=4,y=8,
,解得x=4,y=8,
∴E點坐標為(4,8),故②錯誤;
∵CF=8,OC=10,
∴sin∠COA=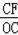
 =
=
 =
=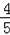
 ,故③正確;
,故③正確;
∵A(10,0),C(6,8),
∴AC=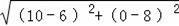
 =4
=4
 ,
,
∵OB•AC=160,
∴OB=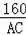
 =
=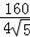
 =8
=8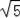
 ,
,
∴AC+OB=4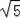
 +8
+8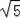
 =12
=12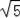
 ,故④正確.
,故④正確.
故選:B.

【點評】本題考查的是反比例函數綜合題,涉及到菱形的性質及反比例函數的性質、銳角三角函數的定義等相關知識,難度適中.


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:
點P(x,y)先向左平移2個單位,再向上平移3個單位得到P′,則點P′的坐標為( )
A.(x﹣2,y+3) B.(x+2,y﹣3) C.(x﹣3,y+2) D.(x+3,y﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,在半徑為6cm的⊙O中,點A是劣弧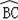
 的中點,點D是優弧
的中點,點D是優弧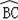
 上一點,且∠D=30°,下列四個結論:
上一點,且∠D=30°,下列四個結論:
①OA⊥BC;②BC=6
 ;③sin∠AOB=
;③sin∠AOB=
 ;④四邊形ABOC是菱形.
;④四邊形ABOC是菱形.
其中正確結論的序號是( )


A.①③ B.①②③④ C.②③④ D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,小俊在A處利用高為1.8米的測角儀AB測得樓EF頂部E的仰角為30°,然后前進12米到達C處,又測得樓頂E的仰角為60°,求樓EF的高度.(結果精確到0.1米)(參考數據:
 =1.414,
=1.414,
 =1.732)
=1.732)


查看答案和解析>>
科目:初中數學 來源: 題型:
某校開展了“我最喜愛的老師”評選活動.確定如下評選方案:有學生和教師代表對4名候選教師進行投票,每票選1名候選教師,每位候選教師得到的教師票數的5倍與學生票數的和作為該教師的總票數.以下是根據學生和教師代表投票結果繪制的統計表和條形統計圖(不完整).
學生投票結果統計表
| 候選教師 | 丁老師 | 俞老師 | 李老師 | 陳老師 |
| 得票數 | 460 | 200 | 140 | 300 |
(1)若共有25位教師代表參加投票,則李老師得到的教師票數是多少?請補全條形統計圖.(畫在答案卷相對應的圖上)
(2)丁老師與李老師得到的學生總票數是600,且丁老師得到的學生票數是李老師得到的學生票數的3倍多40票,求丁老師與李老師得到的學生票數分別是多少?
(3)在(1)、(2)的條件下,若總得票數較高的2名教師推選到市參評,你認為推選到市里的是兩位老師?為什么?


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com