
題目列表(包括答案和解析)
(本題滿分15分)某市物價局調(diào)查了某種治療H1N1流感的常規(guī)藥品在2009年每個月的批發(fā)價格和該藥品在藥店的銷售價格,調(diào)查發(fā)現(xiàn),該藥品的批發(fā)價格按月份以12元/盒為中心價隨某一正弦曲線上下波動,且3月份的批發(fā)價格最高為14元/盒,7月份的批發(fā)價格最低為10元/盒。該藥品在藥店的銷售價格按月份以14元/盒為中心價隨另一正弦曲線上下波動,且5月份的銷售價格最高為16元/盒,9月份的銷售價格最低為12元/盒。
(Ⅰ)求該藥品每盒的批發(fā)價格f(x)和銷售價格g(x)關于月份![]() 的函數(shù)解析式;
的函數(shù)解析式;
(Ⅱ)假設某藥店每月初都購進這種藥品p 盒,且當月售完,求該藥店在2009年哪些月份是盈利的?說明你的理由.
(本小題滿分12分)
| 分 組 | 頻數(shù) | 頻率 |
| [13,14) |
|
|
| [14,15) |
|
|
| [15,16) |
|
|
| [16,17) |
|
|
| [17,18] |
|
|
某班全部![]() 名學生在一次百米測試中,成績?nèi)拷橛?3秒和18秒之間。將測試結果按如下方式分為五組:第一組[13,14);第二組[14,15);…;第五組[17,18],右表是按上述分組方式得到的頻率分布表。
名學生在一次百米測試中,成績?nèi)拷橛?3秒和18秒之間。將測試結果按如下方式分為五組:第一組[13,14);第二組[14,15);…;第五組[17,18],右表是按上述分組方式得到的頻率分布表。
(1)求![]() 及上表中的
及上表中的![]() 的值;
的值;
(2)設m,n是從第一組或第五組中任意抽取的兩名
學生的百米測試成績,求事件“![]() ”的概率.
”的概率.
正整數(shù)按下表排列:
1 2 5 10 17 …
4 3 6 11 18 …
9 8 7 12 19 …
16 15 14 13 20 …
25 24 23 22 21 …
… … … … … …
位于對角線位置的正整數(shù)1,3,7,13,21,…,構成數(shù)列![]() ,則
,則![]() _______;通項公式
_______;通項公式![]() =____________。
=____________。
正整數(shù)按下表排列:
1 2 5 10 17 …
4 3 6 11 18 …
9 8 7 12 19 …
16 15 14 13 20 …
25 24 23 22 21 …
… … … … … …
位于對角線位置的正整數(shù)1,3,7,13,21,…,構成數(shù)列![]() ,則
,則![]() _______;通項公式
_______;通項公式![]() =____________。
=____________。
某花店每天以每枝5元的價格從農(nóng)場購進若干枝玫瑰花,然后以每枝10元的價格出售。如果當天賣不完,剩下的玫瑰花做垃圾處理。
(Ⅰ)若花店一天購進17枝玫瑰花,求當天的利潤y(單位:元)關于當天需求量n(單位:枝,n∈N)的函數(shù)解析式。
(Ⅱ)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
|
日需求量n |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
頻數(shù) |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
(i)假設花店在這100天內(nèi)每天購進17枝玫瑰花,求這100天的日利潤(單位:元)的平均數(shù);
(ii)若花店一天購進17枝玫瑰花,以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率,求當天的利潤不少于75元的概率.
【命題意圖】本題主要考查給出樣本頻數(shù)分別表求樣本的均值、將頻率做概率求互斥事件的和概率,是簡單題.
【解析】(Ⅰ)當日需求量 時,利潤
時,利潤 =85;
=85;
當日需求量 時,利潤
時,利潤 ,
,
∴ 關于
關于 的解析式為
的解析式為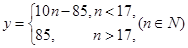 ;
;
(Ⅱ)(i)這100天中有10天的日利潤為55元,20天的日利潤為65元,16天的日利潤為75元,54天的日利潤為85元,所以這100天的平均利潤為
 =76.4;
=76.4;
(ii)利潤不低于75元當且僅當日需求不少于16枝,故當天的利潤不少于75元的概率為

三、選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
A
B
B
D
B
D
A
B
C
B
四、填空題
13.2 14. 31 15. 考數(shù)學試卷(文科).files/image183.gif) 16. 2.
16. 2.
三、解答題
17.17.解:(Ⅰ)考數(shù)學試卷(文科).files/image185.gif)
考數(shù)學試卷(文科).files/image187.gif)
考數(shù)學試卷(文科).files/image189.gif) .
.
考數(shù)學試卷(文科).files/image191.gif) 的最小正周期
的最小正周期考數(shù)學試卷(文科).files/image193.gif) .
.
(Ⅱ)由考數(shù)學試卷(文科).files/image195.gif) 解得
解得
考數(shù)學試卷(文科).files/image197.gif)
∴ 考數(shù)學試卷(文科).files/image095.gif) 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為考數(shù)學試卷(文科).files/image199.gif) 。
。
18.(Ⅰ)解:設“從甲盒內(nèi)取出的2個球均為紅球”為事件考數(shù)學試卷(文科).files/image201.gif) ,“從乙盒內(nèi)取出的2個球均為紅球”為事件
,“從乙盒內(nèi)取出的2個球均為紅球”為事件考數(shù)學試卷(文科).files/image203.gif) .由于事件
.由于事件考數(shù)學試卷(文科).files/image205.gif) 相互獨立,且
相互獨立,且
考數(shù)學試卷(文科).files/image207.gif) ,
,考數(shù)學試卷(文科).files/image209.gif) ,
,
故取出的4個球均為紅球的概率是
考數(shù)學試卷(文科).files/image211.gif) .
.
(Ⅱ)解:設“從甲盒內(nèi)取出的2個球中,1個是紅球,1個是黑球;從乙盒內(nèi)取出的2個紅球為黑球”為事件考數(shù)學試卷(文科).files/image213.gif) ,“從甲盒內(nèi)取出的2個球均為黑球;從乙盒內(nèi)取出的2個球中,1個是紅球,1個是黑球”為事件
,“從甲盒內(nèi)取出的2個球均為黑球;從乙盒內(nèi)取出的2個球中,1個是紅球,1個是黑球”為事件考數(shù)學試卷(文科).files/image215.gif) .由于事件
.由于事件考數(shù)學試卷(文科).files/image217.gif) 互斥,且
互斥,且
考數(shù)學試卷(文科).files/image219.gif) ,
,考數(shù)學試卷(文科).files/image221.gif) .
.
故取出的4個紅球中恰有4個紅球的概率為
考數(shù)學試卷(文科).files/image223.gif) .
.
19.(Ⅰ)取DC的中點E.
∵ABCD是邊長為考數(shù)學試卷(文科).files/image045.gif) 的菱形,
的菱形,考數(shù)學試卷(文科).files/image135.gif) ,∴BE⊥CD.
,∴BE⊥CD.
∵考數(shù)學試卷(文科).files/image137.gif) 平面
平面考數(shù)學試卷(文科).files/image139.gif) , BE
, BE考數(shù)學試卷(文科).files/image037.gif) 平面
平面考數(shù)學試卷(文科).files/image139.gif) ,∴
,∴考數(shù)學試卷(文科).files/image137.gif) BE.
BE.
∴BE⊥平面PDC.∠BPE為求直線PB與平面PDC所成的角.
∵BE=考數(shù)學試卷(文科).files/image226.gif) ,PE=
,PE=考數(shù)學試卷(文科).files/image228.gif) ,∴
,∴考數(shù)學試卷(文科).files/image230.gif) =
=考數(shù)學試卷(文科).files/image232.gif) =
=考數(shù)學試卷(文科).files/image234.gif) .
.
(Ⅱ)連接AC、BD交于點O,因為ABCD是菱形,所以AO⊥BD.
∵考數(shù)學試卷(文科).files/image137.gif) 平面
平面考數(shù)學試卷(文科).files/image139.gif) , AO
, AO考數(shù)學試卷(文科).files/image037.gif) 平面
平面考數(shù)學試卷(文科).files/image139.gif) ,
,
∴考數(shù)學試卷(文科).files/image236.gif) PD. ∴AO⊥平面PDB.
PD. ∴AO⊥平面PDB.
作OF⊥PB于F,連接AF,則AF⊥PB.
故∠AFO就是二面角A-PB-D的平面角.
∵AO=考數(shù)學試卷(文科).files/image226.gif) ,OF=
,OF=考數(shù)學試卷(文科).files/image239.gif) ,∴
,∴考數(shù)學試卷(文科).files/image241.gif) =
=考數(shù)學試卷(文科).files/image243.gif) .
.
20.解:(1)令考數(shù)學試卷(文科).files/image245.gif) 得所求增區(qū)間為
得所求增區(qū)間為考數(shù)學試卷(文科).files/image247.gif) ,
,考數(shù)學試卷(文科).files/image249.gif) 。
。
(2)要使當考數(shù)學試卷(文科).files/image250.gif) 時
時考數(shù)學試卷(文科).files/image251.gif) 恒成立,只要當
恒成立,只要當考數(shù)學試卷(文科).files/image250.gif) 時
時 考數(shù)學試卷(文科).files/image253.gif) 。
。
由(1)知
當考數(shù)學試卷(文科).files/image255.gif) 時,
時,考數(shù)學試卷(文科).files/image256.gif) 是增函數(shù),
是增函數(shù),考數(shù)學試卷(文科).files/image258.gif) ;
;
當考數(shù)學試卷(文科).files/image260.gif) 時,
時,考數(shù)學試卷(文科).files/image256.gif) 是減函數(shù),
是減函數(shù),考數(shù)學試卷(文科).files/image262.gif) ;
;
當考數(shù)學試卷(文科).files/image264.gif) 時,
時,考數(shù)學試卷(文科).files/image256.gif) 是增函數(shù),
是增函數(shù),考數(shù)學試卷(文科).files/image266.gif)
由考數(shù)學試卷(文科).files/image268.gif) ,因此
,因此考數(shù)學試卷(文科).files/image266.gif) 故
故考數(shù)學試卷(文科).files/image270.gif) 。
。
21. 證明:由考數(shù)學試卷(文科).files/image272.gif) 是關于x的方程
是關于x的方程考數(shù)學試卷(文科).files/image274.gif) 的兩根得
的兩根得
考數(shù)學試卷(文科).files/image276.gif) 。
。
考數(shù)學試卷(文科).files/image278.gif)
考數(shù)學試卷(文科).files/image280.gif) ,
,考數(shù)學試卷(文科).files/image282.gif)
考數(shù)學試卷(文科).files/image284.gif) 是等差數(shù)列。
是等差數(shù)列。
(2)由(1)知考數(shù)學試卷(文科).files/image286.gif)
考數(shù)學試卷(文科).files/image288.gif)
考數(shù)學試卷(文科).files/image290.gif) 。
。
考數(shù)學試卷(文科).files/image292.gif) 。
。
又考數(shù)學試卷(文科).files/image294.gif) 符合上式,
符合上式,考數(shù)學試卷(文科).files/image296.gif) 。
。
(3)考數(shù)學試卷(文科).files/image298.gif) ①
①
考數(shù)學試卷(文科).files/image300.gif) ②
②
①―②得 考數(shù)學試卷(文科).files/image302.gif) 。
。
考數(shù)學試卷(文科).files/image304.gif)
考數(shù)學試卷(文科).files/image306.gif)
考數(shù)學試卷(文科).files/image308.gif) 。
。
22. (1)∵考數(shù)學試卷(文科).files/image310.gif)
∴考數(shù)學試卷(文科).files/image312.gif)
令考數(shù)學試卷(文科).files/image314.gif) ,∴
,∴考數(shù)學試卷(文科).files/image316.gif) 或
或考數(shù)學試卷(文科).files/image318.gif)
若考數(shù)學試卷(文科).files/image320.gif) ,
,
在點考數(shù)學試卷(文科).files/image316.gif) 附近,當
附近,當考數(shù)學試卷(文科).files/image322.gif) 時,
時,考數(shù)學試卷(文科).files/image324.gif) ;當
;當考數(shù)學試卷(文科).files/image326.gif) 時,
時,考數(shù)學試卷(文科).files/image328.gif)
∴考數(shù)學試卷(文科).files/image316.gif) 是函數(shù)
是函數(shù)考數(shù)學試卷(文科).files/image173.gif) 的極小值點,極小值為
的極小值點,極小值為考數(shù)學試卷(文科).files/image330.gif) ;
;
在點考數(shù)學試卷(文科).files/image318.gif) 附近,當
附近,當考數(shù)學試卷(文科).files/image332.gif) 時,
時,考數(shù)學試卷(文科).files/image328.gif) ;當
;當考數(shù)學試卷(文科).files/image335.gif) 時,
時,考數(shù)學試卷(文科).files/image324.gif)
∴考數(shù)學試卷(文科).files/image318.gif) 是函數(shù)
是函數(shù)考數(shù)學試卷(文科).files/image173.gif) 的極大值點,極大值為
的極大值點,極大值為考數(shù)學試卷(文科).files/image338.gif)
若考數(shù)學試卷(文科).files/image340.gif) ,易知,
,易知,
考數(shù)學試卷(文科).files/image316.gif) 是函數(shù)
是函數(shù)考數(shù)學試卷(文科).files/image173.gif) 的極大值點,極大值為
的極大值點,極大值為考數(shù)學試卷(文科).files/image330.gif) ;
;
考數(shù)學試卷(文科).files/image318.gif) 是函數(shù)
是函數(shù)考數(shù)學試卷(文科).files/image173.gif) 的極小值點,極小值為
的極小值點,極小值為考數(shù)學試卷(文科).files/image338.gif)
(2)若在考數(shù)學試卷(文科).files/image175.gif) 上至少存在一點
上至少存在一點考數(shù)學試卷(文科).files/image177.gif) 使得
使得考數(shù)學試卷(文科).files/image179.gif) 成立,
成立,
則考數(shù)學試卷(文科).files/image342.gif) 在
在考數(shù)學試卷(文科).files/image175.gif) 上至少存在一解,即
上至少存在一解,即考數(shù)學試卷(文科).files/image344.gif) 在
在考數(shù)學試卷(文科).files/image175.gif) 上至少存在一解
上至少存在一解
由(1)知,
當考數(shù)學試卷(文科).files/image340.gif) 時,函數(shù)
時,函數(shù)考數(shù)學試卷(文科).files/image173.gif) 在區(qū)間
在區(qū)間考數(shù)學試卷(文科).files/image175.gif) 上遞增,且極小值為
上遞增,且極小值為考數(shù)學試卷(文科).files/image346.gif)
∴此時考數(shù)學試卷(文科).files/image344.gif) 在
在考數(shù)學試卷(文科).files/image175.gif) 上至少存在一解;
上至少存在一解;
當考數(shù)學試卷(文科).files/image320.gif) 時,函數(shù)
時,函數(shù)考數(shù)學試卷(文科).files/image173.gif) 在區(qū)間
在區(qū)間考數(shù)學試卷(文科).files/image349.gif) 上遞增,在
上遞增,在考數(shù)學試卷(文科).files/image351.gif) 上遞減,
上遞減,
∴要滿足條件應有函數(shù)考數(shù)學試卷(文科).files/image173.gif) 的極大值
的極大值考數(shù)學試卷(文科).files/image353.gif) ,即
,即考數(shù)學試卷(文科).files/image355.gif)
綜上,實數(shù)考數(shù)學試卷(文科).files/image045.gif) 的取值范圍為
的取值范圍為考數(shù)學試卷(文科).files/image340.gif) 或
或考數(shù)學試卷(文科).files/image355.gif) 。
。
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com