題目列表(包括答案和解析)
設函數
在
處取得極值，且曲線
在點
處的切線垂直于直線
.
(Ⅰ) 求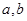
的值；
（Ⅱ）求曲線和直線所圍成的封閉圖形的面積；
（Ⅲ）設函數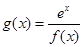
，若方程
有三個不相等的實根，求
的取值范圍.
【解析】本試題主要考查了導數的運用。利用導數求解曲邊梯形的面積，以及求解函數與方程的根的問題的綜合運用。
在
處取得極值，且曲線
在點
處的切線垂直于直線
.
的值；和直線所圍成的封閉圖形的面積；
，若方程
有三個不相等的實根，求
的取值范圍.（12分）已知函數
在
處取得極值，且在點
處的切線的斜率為2。
（1）求a、b的值；
（2）求函數
的單調區間和極值；
（3）若關于x的方程
在
上恰有兩個不相等的實數根，求實數m的取值范圍。
一、選擇題（每小題5分，共50分）
二、填空題（每小題4分，共28分）
三、解答題
18.解：（Ⅰ）由已有
(4分)
(6分)
（Ⅱ）由（1）
且
(8分)
所以
（10分）
（12分）
（14分）
19.解：（Ⅰ）同學甲同學恰好投4次達標的概率
(4分)
（Ⅱ）
可取的值是
（6分）
（8分）
（10分）
的分布列為
3
4
5
（12分）
所以的數學期望為
（14分）
20.解:（Ⅰ）∵PA⊥底面ABCD，BC
平面AC，∴PA⊥BC
∵∠ACB=90°，∴BC⊥AC，又PA∩AC=A，∴BC⊥平面PAC （4分）
（Ⅱ）取CD的中點E，則AE⊥CD，∴AE⊥AB，又PA⊥底面ABCD，∴PA⊥AE
建立如圖所示空間直角坐標系，則
A（0，，0，0），P（0，0，
），C（
，0），D（
，0）
，
，
(6分)
易求
為平面PAC的一個法向量.
為平面PDC的一個法向量
（9分）
∴cos
故二面角D-PC-A的正切值為2. (11分)
（Ⅲ）設
,則
,
解得點
,即
（13分）
由
得
(不合題意舍去)或
所以當
為
的中點時,直線
與平面
所成角的正弦值為
（15分）
21.解：（Ⅰ）設直線
的方程為：
由
得
，所以的方程為
(4分)
由
得
點的坐標為
.
可求得拋物線的標準方程為
.
（6分）
（Ⅱ）設直線
的方程為
，代入拋物線方程并整理得
(8分)
設
則
設
，則
(11分)
當
時上式是一個與
無關的常數.
所以存在定點
，相應的常數是
.
(14分)
22．解：（Ⅰ）當
時
(2分)
在
上遞增，在
上遞減
所以
在0和2處分別達到極大和極小，由已知有
且
，因而
的取值范圍是
.
(4分)
（Ⅱ）當
時，
即
(7分)
則
，
在
上遞減，在
上遞增.
上遞增
故
(10分)
⊥
，即
=
，
（12分）
，
(x)=0的兩根可得，
≥2
，這與
與直線
不可能垂直.
(15分)