
題目列表(包括答案和解析)
(本題滿分15分)如圖,在底面是菱形的四棱錐P—ABCD中,∠ABC=600,PA=AC=a,PB=PD= ,點(diǎn)E在PD上,且PE:ED=2:1.
,點(diǎn)E在PD上,且PE:ED=2:1.
(1)證明:PA⊥平面ABCD;
(2)求以AC為棱,EAC與DAC為面的二面角 的大小.
的大小.
 (本題滿分15分)如圖,在底面是菱形的四棱錐P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=
(本題滿分15分)如圖,在底面是菱形的四棱錐P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=![]() ,點(diǎn)E在PD上,且PE:ED=2:1.
,點(diǎn)E在PD上,且PE:ED=2:1.
(1)證明:PA⊥平面ABCD;
(2)求以AC為棱,EAC與DAC為面的二面角![]() 的大小.
的大小.
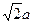 ,點(diǎn)E在PD上,且PE:ED=2:1.
,點(diǎn)E在PD上,且PE:ED=2:1.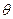 的大小.
的大小. (本題滿分15分)如圖,已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的中點(diǎn).
的中點(diǎn).
 (Ⅰ)證明:
(Ⅰ)證明:![]() ;
;
(Ⅱ)若![]() 為
為![]() 上的動(dòng)點(diǎn),
上的動(dòng)點(diǎn),![]() 與平面
與平面![]() 所成最大角的正切值為
所成最大角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
(本小題滿分15分)如圖,在四棱錐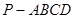 中,底面
中,底面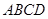 是正方形,側(cè)棱
是正方形,側(cè)棱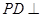 底面
底面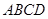 ,
,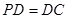 ,
,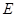 是
是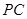 的中點(diǎn),作
的中點(diǎn),作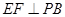 交
交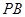 于點(diǎn)
于點(diǎn)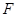
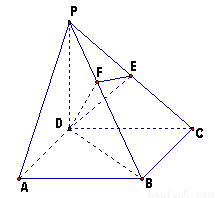
(1)證明: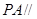 平面
平面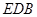 .
.
(2)證明: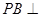 平面
平面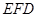 .
.
(3)求二面角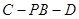 的大小.
的大小.
一、選擇題(每小題5分,共50分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image326.gif)
二、填空題(每小題4分,共28分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image328.gif)
三、解答題
18.解:(Ⅰ)由已有
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image330.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image165.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image333.gif)
(4分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image335.gif)
(6分)
(Ⅱ)由(1)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image337.gif) 且
且州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image339.gif) (8分)
(8分)
所以州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image341.gif) (10分)
(10分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image343.gif) (12分)
(12分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image345.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image347.gif) (14分)
(14分)
19.解:(Ⅰ)同學(xué)甲同學(xué)恰好投4次達(dá)標(biāo)的概率州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image349.gif) (4分)
(4分)
(Ⅱ)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image351.gif) 可取的值是
可取的值是州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image353.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image355.gif) (6分)
(6分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image357.gif) (8分)
(8分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image359.gif) (10分)
(10分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image351.gif) 的分布列為
的分布列為
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image362.gif)
3
4
5
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image364.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image366.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image368.gif)
(12分)
所以州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image351.gif) 的數(shù)學(xué)期望為
的數(shù)學(xué)期望為州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image371.gif) (14分)
(14分)
20.解:(Ⅰ)∵PA⊥底面ABCD,BC州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image373.gif) 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC (4分)
(Ⅱ)取CD的中點(diǎn)E,則AE⊥CD,∴AE⊥AB,又PA⊥底面ABCD,∴PA⊥AE
建立如圖所示空間直角坐標(biāo)系,則
A(0,,0,0),P(0,0,州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image245.gif) ),C(
),C(州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image376.gif) ,0),D(
,0),D(州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image378.gif) ,0)
,0)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image380.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image382.gif) ,
,州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image384.gif) ,
,州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image386.gif) (6分)
(6分)
易求州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image388.gif) 為平面PAC的一個(gè)法向量.
為平面PAC的一個(gè)法向量.
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image390.gif) 為平面PDC的一個(gè)法向量
(9分)
為平面PDC的一個(gè)法向量
(9分)
∴cos州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image392.gif)
故二面角D-PC-A的正切值為2. (11分)
(Ⅲ)設(shè)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image394.gif) ,則
,則
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image396.gif) ,
,
解得點(diǎn)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image398.gif) ,即
,即州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image400.gif) (13分)
(13分)
由州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image402.gif) 得
得州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image404.gif) (不合題意舍去)或
(不合題意舍去)或州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image406.gif)
所以當(dāng)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image249.gif) 為
為州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image251.gif) 的中點(diǎn)時(shí),直線
的中點(diǎn)時(shí),直線州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image410.gif) 與平面
與平面州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image262.gif) 所成角的正弦值為
所成角的正弦值為州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image413.gif) (15分)
(15分)
21.解:(Ⅰ)設(shè)直線州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image273.gif) 的方程為:
的方程為:州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image416.gif)
由州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image418.gif) 得
得州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image420.gif) ,所以
,所以州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image273.gif) 的方程為
的方程為州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image423.gif) (4分)
(4分)
由州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image425.gif) 得
得州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image277.gif) 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image428.gif) .
.
可求得拋物線的標(biāo)準(zhǔn)方程為州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image430.gif) .
(6分)
.
(6分)
(Ⅱ)設(shè)直線州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image282.gif) 的方程為
的方程為州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image433.gif) ,代入拋物線方程并整理得
,代入拋物線方程并整理得州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image435.gif) (8分)
(8分)
設(shè)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image437.gif) 則
則州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image439.gif)
設(shè)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image441.gif) ,則
,則州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image443.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image445.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image447.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image449.gif)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image451.gif) (11分)
(11分)
當(dāng)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image453.gif) 時(shí)上式是一個(gè)與
時(shí)上式是一個(gè)與州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image086.gif) 無(wú)關(guān)的常數(shù).
無(wú)關(guān)的常數(shù).
所以存在定點(diǎn)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image456.gif) ,相應(yīng)的常數(shù)是
,相應(yīng)的常數(shù)是州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image458.gif) .
(14分)
.
(14分)
22.解:(Ⅰ)當(dāng)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image460.gif) 時(shí)
時(shí)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image462.gif) (2分)
(2分)
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image464.gif) 在
在州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image466.gif) 上遞增,在
上遞增,在州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image468.gif) 上遞減
上遞減
所以州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image192.gif) 在0和2處分別達(dá)到極大和極小,由已知有
在0和2處分別達(dá)到極大和極小,由已知有
州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image471.gif) 且
且州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image473.gif) ,因而
,因而州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image302.gif) 的取值范圍是
的取值范圍是州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image476.gif) .
(4分)
.
(4分)
(Ⅱ)當(dāng)州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image304.gif) 時(shí),
時(shí),州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image479.gif) 即
即州市2009年高三年級(jí)第一次調(diào)考試題%20數(shù)學(xué)理科.files/image481.gif)