題目列表(包括答案和解析)
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 3 |
| P |
| P |
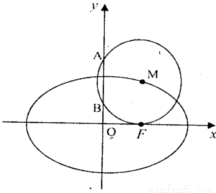
(本小題滿分14分)已知點F橢圓E：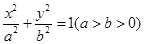
的右焦點，點M在橢圓E上，以M為圓心的圓與x軸切于點F，與y軸交于A、B兩點，且
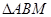是邊長為2的正三角形；又橢圓E上的P、Q兩點關于直線
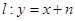對稱.
（1）求橢圓E的方程；（2）當直線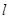
過點（
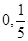）時，求直線PQ的方程；
(3)若點C是直線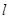上一點，且
=
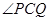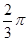，求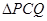
面積的最大值.
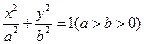的右焦點，點M在橢圓E上，以M為圓心的圓與x軸切于點F，與y軸交于A、B兩點，且
是邊長為2的正三角形；又橢圓E上的P、Q兩點關于直線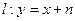
對稱.
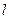過點（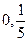
）時，求直線PQ的方程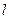；上一點，且
=
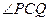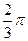，求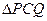
面積的最大值.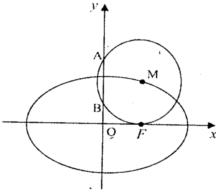
1-10．CDBBA CACBD
11．
12. ①③④ 13.-2或1 14. 
、
15.2 16. 
17.
.
18．
解：（1）由已知
7分
（2）由
10分
由余弦定理得
14分
19.（1）證明：∵PA⊥底面ABCD，BC
平面AC，∴PA⊥BC, 3分
∵∠ACB=90°，∴BC⊥AC，又PA∩AC=A，∴BC⊥平面PAC. 5分
（2）解：過C作CE⊥AB于E，連接PE，
∵PA⊥底面ABCD，∴CE⊥面PAB，
∴直線PC與平面PAB所成的角為
， 10分
∵AD=CD=1，∠ADC=60°，∴AC=1，PC=2,
中求得CE=
，∴
. 14分
20．解：（1）由
①，得
②，
②-①得：
. 4分
（2）由
求得
. 7分
∴
，
11分
∴
.
14分
21．解：
（1）由
得c=1 1分
， 4分
5分
得
，
時取得極值.由
，
得
∴
. 8分
，
，∴當
時，
， 
在
上遞減. 12分
∴函數
的零點有且僅有1個 15分
，由已知
，
， 2分
，
6分
點 B（0，t），點
， 7分
， 9分
，
，
，
， 13分
，又
時，
，
面積的最小值為
15分