
題目列表(包括答案和解析)
設(shè)函數(shù)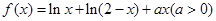 .
.
(Ⅰ) 當(dāng) 時(shí),求
時(shí),求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ) 若 在
在 上的最大值為
上的最大值為 ,求
,求 的值.
的值.
【解析】第一問(wèn)中利用函數(shù) 的定義域?yàn)椋?,2),
的定義域?yàn)椋?,2), .
.
當(dāng)a=1時(shí), 所以
所以 的單調(diào)遞增區(qū)間為(0,
的單調(diào)遞增區(qū)間為(0, ),單調(diào)遞減區(qū)間為(
),單調(diào)遞減區(qū)間為( ,2);
,2);
第二問(wèn)中,利用當(dāng) 時(shí),
時(shí), >0, 即
>0, 即 在
在 上單調(diào)遞增,故
上單調(diào)遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
解:函數(shù) 的定義域?yàn)椋?,2),
的定義域?yàn)椋?,2), .
.
(1)當(dāng) 時(shí),
時(shí), 所以
所以 的單調(diào)遞增區(qū)間為(0,
的單調(diào)遞增區(qū)間為(0, ),單調(diào)遞減區(qū)間為(
),單調(diào)遞減區(qū)間為( ,2);
,2);
(2)當(dāng) 時(shí),
時(shí), >0, 即
>0, 即 在
在 上單調(diào)遞增,故
上單調(diào)遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
已知函數(shù) =
= .
.
(Ⅰ)當(dāng) 時(shí),求不等式
時(shí),求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范圍.
的取值范圍.
【命題意圖】本題主要考查含絕對(duì)值不等式的解法,是簡(jiǎn)單題.
【解析】(Ⅰ)當(dāng) 時(shí),
時(shí), =
= ,
,
當(dāng) ≤2時(shí),由
≤2時(shí),由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
當(dāng)2< <3時(shí),
<3時(shí), ≥3,無(wú)解;
≥3,無(wú)解;
當(dāng) ≥3時(shí),由
≥3時(shí),由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集為{
≥3的解集為{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
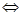
 ,
,
當(dāng) ∈[1,2]時(shí),
∈[1,2]時(shí), =
= =2,
=2,
∴ ,有條件得
,有條件得 且
且 ,即
,即 ,
,
故滿(mǎn)足條件的 的取值范圍為[-3,0]
的取值范圍為[-3,0]
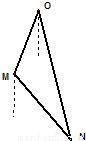
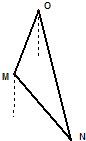 如圖所示,正在亞丁灣執(zhí)行護(hù)航任務(wù)的某導(dǎo)彈護(hù)衛(wèi)艦,突然收到一艘商船的求救信號(hào),緊急前往相關(guān)海域.到達(dá)相關(guān)海域O處后發(fā)現(xiàn),在南偏西20°、5海里外的洋面M處有一條海盜船,它正以每小時(shí)20海里的速度向南偏東40°的方向逃竄.某導(dǎo)彈護(hù)衛(wèi)艦當(dāng)即施放載有突擊隊(duì)員的快艇進(jìn)行攔截,快艇以每小時(shí)30海里的速度向南偏東θ°的方向全速追擊.請(qǐng)問(wèn):快艇能否追上海盜船?如果能追上,請(qǐng)求出sin(θ°+20°)的值;如果未能追上,請(qǐng)說(shuō)明理由.(假設(shè)海面上風(fēng)平浪靜、海盜船逃竄的航向不變、快艇運(yùn)轉(zhuǎn)正常無(wú)故障等)
如圖所示,正在亞丁灣執(zhí)行護(hù)航任務(wù)的某導(dǎo)彈護(hù)衛(wèi)艦,突然收到一艘商船的求救信號(hào),緊急前往相關(guān)海域.到達(dá)相關(guān)海域O處后發(fā)現(xiàn),在南偏西20°、5海里外的洋面M處有一條海盜船,它正以每小時(shí)20海里的速度向南偏東40°的方向逃竄.某導(dǎo)彈護(hù)衛(wèi)艦當(dāng)即施放載有突擊隊(duì)員的快艇進(jìn)行攔截,快艇以每小時(shí)30海里的速度向南偏東θ°的方向全速追擊.請(qǐng)問(wèn):快艇能否追上海盜船?如果能追上,請(qǐng)求出sin(θ°+20°)的值;如果未能追上,請(qǐng)說(shuō)明理由.(假設(shè)海面上風(fēng)平浪靜、海盜船逃竄的航向不變、快艇運(yùn)轉(zhuǎn)正常無(wú)故障等)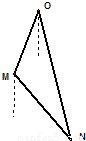
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com