題目列表(包括答案和解析)
設(shè)
圖像上任意二點(diǎn)，且
，已知點(diǎn)M的縱坐標(biāo)為
（1）求證：M點(diǎn)的坐標(biāo)為定值；
（2）定義
；
（3）若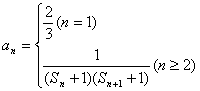
，是否存在實(shí)數(shù)λ，對(duì)于任意n∈N*，都有
恒成立，若存在求出λ，不存在說明理由.
設(shè)
圖像上任意二點(diǎn)，且
，已知點(diǎn)M的縱坐標(biāo)為
（1）求證：M點(diǎn)的坐標(biāo)為定值；
（2）定義
；
（3）若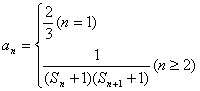
，是否存在實(shí)數(shù)λ，對(duì)于任意n∈N*，都有
恒成立，若存在求出λ，不存在說明理由.
已知函數(shù)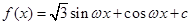
（
，
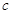是實(shí)數(shù)常數(shù)）的圖像上的一個(gè)最高點(diǎn)
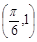，與該最高點(diǎn)最近的一個(gè)最低點(diǎn)是
，
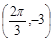(1)求函數(shù)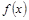
的解析式及其單調(diào)增區(qū)間；
(2)在銳角三角形△ABC中，角A、B、C所對(duì)的邊分別為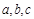
，且
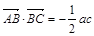，角A的取值范圍是區(qū)間M，當(dāng)
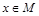時(shí)，試求函數(shù)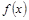的取值范圍.
（
，
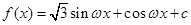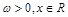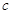是實(shí)數(shù)常數(shù)）的圖像上的一個(gè)最高點(diǎn)
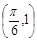，與該最高點(diǎn)最近的一個(gè)最低點(diǎn)是
，
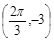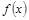的解析式及其單調(diào)增區(qū)間；
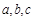，且
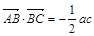，角A的取值范圍是區(qū)間M，當(dāng)
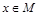時(shí)，試求函數(shù)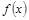的取值范圍.已知函數(shù)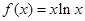
（Ⅰ）求函數(shù)
的圖像在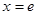
處的切線方程；
（Ⅱ）設(shè)實(shí)數(shù)
，求函數(shù)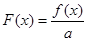
在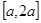
上的最小值.
一、選擇題：本大題共10小題，每小題5分，共50分．
題號(hào)
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空題：本大題7小題，每小題4分，共28分．
11、
； 12、 
； 13、
； 14、
； 15、
； 16、
；17、
。
三、解答題
18、（1）略 ……………………………………………………………………（7分）
（2）
就是二面角
的平面角，即
，
…………………………………………………………………（9分）
取
中點(diǎn)
，則
平面
，
就是
與平面所成的角。 …………………………（11分）
，
，
所以與平面所成的角的大小為
。 …………………………（14分）
（用向量方法，相應(yīng)給分）
19、（1）
，
，
…………（7分）
（2）
，當(dāng)
時(shí)，
；當(dāng)
時(shí)，
，而
，
……………………………………………（14分）
20、（1）當(dāng)
，當(dāng)k＝1時(shí)，
……………………………………… （7分）
（2）由已知
，又設(shè)
，則
，
知當(dāng)
時(shí)，
為增函數(shù)，則知
為增函數(shù)。…………………（14分）
（用導(dǎo)數(shù)法相應(yīng)給分）
21、.解：（1）、設(shè)
，則
，
∵點(diǎn)P分
所成的比為
∴ 
∴ 
∴
代入
中，得
為P點(diǎn)的軌跡方程．
當(dāng)
時(shí)，軌跡是圓． …………………………………………………（7分）
（2）、由題設(shè)知直線l的方程為
， 設(shè)
聯(lián)立方程組
，消去
得：
∵ 方程組有兩解 ∴ 
且
∴
或
且
∵
∴
又 ∵ 
∴ 
解得
（舍去）或
∴ 曲線C的方程是
……………………………………………（14分）
22、解（1）
………………………………………………（5分）
猜想 
， …………………………………………………………（7分）
證明（略） ……………………………………………………………………（10分）
（2）
，要使
恒成立，
恒成立
即
恒成立.
（i）當(dāng)
為奇數(shù)時(shí)，即
恒成立， 又
的最小值為1，
（ii）當(dāng)為偶數(shù)時(shí)，即
恒成立， 又
的最大值為
，
即
，又
，
為整數(shù)，
∴
，使得對(duì)任意
，都有
…………………………………（ 16分）
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com