
已知函數(shù)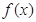 =
=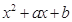 ,
,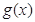 =
=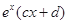 ,若曲線
,若曲線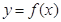 和曲線
和曲線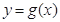 都過點P(0,2),且在點P處有相同的切線
都過點P(0,2),且在點P處有相同的切線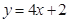 .
.
(Ⅰ)求 ,
,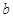 ,
,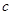 ,
,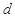 的值;
的值;
(Ⅱ)若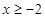 時,
時,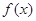 ≤
≤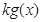 ,求
,求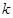 的取值范圍.
的取值范圍.
(Ⅰ)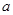 =4,
=4,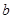 =2,
=2,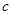 =2,
=2,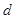 =2;(Ⅱ)
=2;(Ⅱ)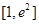
【解析】
試題分析:(Ⅰ)求四個參數(shù)的值,需尋求四個獨立的條件,依題意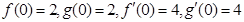
代入即可求出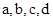 的值;(Ⅱ)構(gòu)造函數(shù),轉(zhuǎn)化為求函數(shù)的最值,記
的值;(Ⅱ)構(gòu)造函數(shù),轉(zhuǎn)化為求函數(shù)的最值,記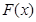 =
= =
=
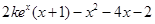 (
(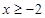 ),由已知
),由已知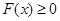 ,只需令
,只需令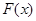 的最小值大于0即可,先求
的最小值大于0即可,先求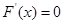 的根,得
的根,得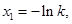
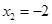 ,只需討論
,只需討論 和定義域
和定義域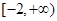 的位置,分三種情況進行,當
的位置,分三種情況進行,當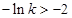 時,將定義域分段,分別研究其導(dǎo)函數(shù)
時,將定義域分段,分別研究其導(dǎo)函數(shù)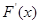 的符號,進而求最小值;當
的符號,進而求最小值;當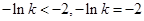 時,
時,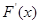 的符號確定,故此時函數(shù)
的符號確定,故此時函數(shù)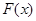 具有單調(diào)性,利用單調(diào)性求其最小值即可.
具有單調(diào)性,利用單調(diào)性求其最小值即可.
試題解析:(Ⅰ) 由已知得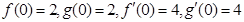 ,而
,而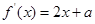
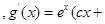
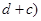 ,代入得
,代入得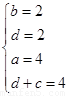 ,故
,故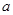 =4,
=4,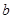 =2,
=2,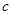 =2,
=2,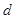 =2;
=2;
(Ⅱ)由(Ⅰ)知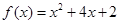
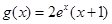 ,
,
設(shè)函數(shù)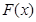 =
= =
=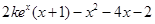 (
(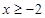 ),
),
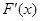 =
=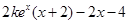 =
=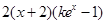 ,
由題設(shè)知
,
由題設(shè)知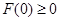 ,即
,即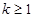 ,令
,令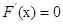 ,得
,得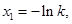
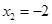 ,
,
(1)若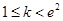 ,則
,則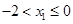 ,∴當
,∴當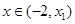 時,
時,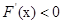 ,當
,當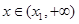 時,
時,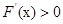 ,記
,記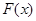 在
在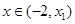 時單調(diào)遞減,
時單調(diào)遞減,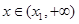 時單調(diào)遞增,故
時單調(diào)遞增,故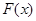 在
在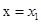 時取最小值
時取最小值 ,而
,而
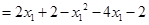
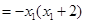
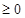 ,∴當
,∴當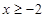 時,
時,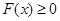 ,即
,即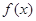 ≤
≤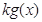 ;
;
(2)若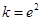 ,則
,則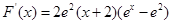 ,∴當
,∴當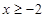 時,
時,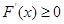 ,∴
,∴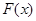 在
在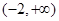 單調(diào)遞增,而
單調(diào)遞增,而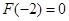 .∴當
.∴當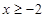 時,
時,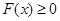 ,即
,即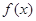 ≤
≤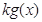 ;
;
(3)若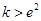 時,
時,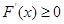 ,則
,則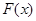 在
在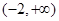 單調(diào)遞增,而
單調(diào)遞增,而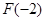 =
=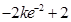 =
=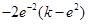 <0,
<0,
∴當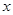 ≥-2時,
≥-2時, ≤
≤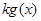 不可能恒成立,
不可能恒成立,
綜上所述,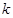 的取值范圍為[1,
的取值范圍為[1,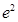 ].
].
考點:1、導(dǎo)數(shù)的幾何意義;2、導(dǎo)數(shù)在單調(diào)性上的應(yīng)用;3、函數(shù)的極值和最值.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
| p | x |
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年福建省福州市八縣(市)一中高三(上)期中數(shù)學試卷(文科)(解析版) 題型:解答題
 -2lnx、
-2lnx、查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年福建省龍巖市高三(上)期末質(zhì)量檢查一級達標數(shù)學試卷(文科)(解析版) 題型:解答題
 -2lnx、
-2lnx、查看答案和解析>>
科目:高中數(shù)學 來源:2011年福建省莆田十中高三適應(yīng)性考試數(shù)學試卷(文科)(解析版) 題型:解答題
 -2lnx、
-2lnx、查看答案和解析>>
科目:高中數(shù)學 來源:2011年福建省寧德市古田縣高三適應(yīng)性測試數(shù)學試卷(文科)(解析版) 題型:解答題
 -2lnx、
-2lnx、查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com