
(本小題滿分13分)
為回饋顧客,某商場擬通過摸球兌獎的方式對1000位顧客進行獎勵,規定:每位顧客從一個裝有4個標有面值的球的袋中一次性隨機摸出2個球,球上所標的面值之和為該顧客所獲的獎勵額.
(1)若袋中所裝的4個球中有1個所標的面值為50元,其余3個均為10元,求
①顧客所獲的獎勵額為60元的概率
②顧客所獲的獎勵額的分布列及數學期望;
(2)商場對獎勵總額的預算是60000元,并規定袋中的4個球只能由標有面值10元和50元的兩種球組成,或標有面值20元和40元的兩種球組成.為了使顧客得到的獎勵總額盡可能符合商場的預算且每位顧客所獲的獎勵額相對均衡,請對袋中的4個球的面值給出一個合適的設計,并說明理由.
(1)  ,參考解析;(2)參考解析
,參考解析;(2)參考解析
解析試題分析:(1)由袋中所裝的4個球中有1個所標的面值為50元,其余3個均為10元,又規定每位顧客從
一個裝有4個標有面值的球的袋中一次性隨機摸出2個球,球上所標的面值之和為該顧客所獲的獎勵額..由獲得60元的事件數 除以總的事件數
除以總的事件數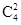 即可. 顧客獲得獎勵有兩種情況20元,60元.分別計算出他們的概率,再利用數學期望的公式即可得結論.
即可. 顧客獲得獎勵有兩種情況20元,60元.分別計算出他們的概率,再利用數學期望的公式即可得結論.
(2) 根據商場的預算,每個顧客的平均獎勵為60元.根據題意有兩種獲獎勵的情況,確定符合題意的方案,分別僅有一種.再分別計算出兩種方案相應的概率以及求出數學期望和方差.即可得到結論.
試題解析:(1)設顧客所獲的獎勵為X. ①依題意,得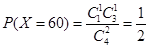 .即顧客所獲得的獎勵額為60元的概率為
.即顧客所獲得的獎勵額為60元的概率為 .
.
②依題意,得X的所有可能取值為20,60. 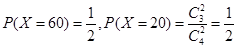 .即X的分布列為
.即X的分布列為
所以顧客所獲得的獎勵額的期望為X 20 60 P 0.5 0.5 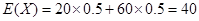 (元).
(元).
(2)根據商場的預算,每個顧客的平均獎勵為60元.所以先尋找期望為60元的可能方案.對于面值由10元和50元組成的情況,如果選擇(10,10,10,50)的方案,因為60元是面值之和的最大值,所以期望不可能為60元;如果選擇(50,50,50,10)的方案,因為60元是面值之和的最小值,所以數學期望也不可能為60元,因此可能的方案是(10,10,50,50),記為方案1.對于面值由20元和40元組成的情況,同理可排除(20,20,20,40)和(40,40,40,20)的方案,所以可能的方案是(20,20,40,40),記為方案2.以下是對兩個方案的分析:對于方案1,即方案(10,10,50,50),設顧客所獲的獎勵為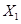 ,則
,則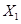 的分布列為
的分布列為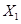
20 60 100 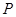
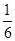
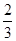
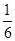
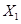 的期望為
的期望為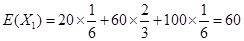 ,
,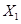 的方差為
的方差為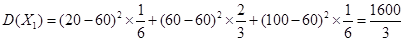 .
.
對于方案2,即方案(20,20,40,40),設顧客所獲的獎勵為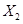 ,則
,則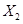 的分布列為
的分布列為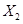
40 60 80 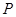
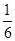
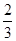
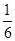
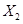 的期望為
的期望為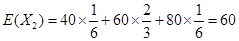 ,
, 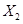 的方差為
的方差為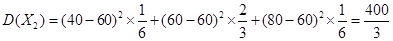 .由于兩種方案的獎勵額都符合要求,但方案2獎勵的方差比方案1的小,所以應該選擇方案2.
.由于兩種方案的獎勵額都符合要求,但方案2獎勵的方差比方案1的小,所以應該選擇方案2.
考點:1.概率.2.統計.3.數學期望,方差.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:解答題
現有編號分別為1,2,3,4,5的五個不同的語文題和編號分別為6,7,8,9,的四個不同的數學題。甲同學從這九個題中一次隨機抽取兩道題,每題被抽到的概率是相等的,用符號(x,y)表示事件“抽到的兩題的編號分別為x、y,且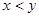 ”
”
(1)共有多少個基本事件?并列舉出來;
(2)求甲同學所抽取的兩題的編號之和小于17但不小于11的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
將連續正整數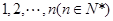 從小到大排列構成一個數
從小到大排列構成一個數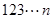 ,
,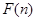 為這個數的位數(如
為這個數的位數(如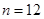 時,此數為
時,此數為 ,共有15個數字,
,共有15個數字, ),現從這個數中隨機取一個數字,
),現從這個數中隨機取一個數字,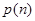 為恰好取到0的概率.
為恰好取到0的概率.
(1)求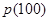 ;
;
(2)當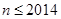 時,求
時,求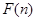 的表達式;
的表達式;
(3)令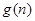 為這個數中數字0的個數,
為這個數中數字0的個數,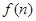 為這個數中數字9的個數,
為這個數中數字9的個數,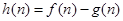 ,
, ,求當
,求當 時
時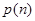 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某大學志愿者協會有6名男同學,4名女同學.在這10名同學中,3名同學來自數學學院,其余7名同學來自物理、化學等其他互不相同的七個學院.現從這10名同學中隨機選取3名同學,到希望小學進行支教活動(每位同學被選到的可能性相同).
(1)求選出的3名同學是來自互不相同學院的概率;
(2)設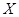 為選出的3名同學中女同學的人數,求隨機變量
為選出的3名同學中女同學的人數,求隨機變量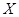 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某超市在節日期間進行有獎促銷,規定凡在該超市購物滿400元的顧客,均可獲得一次摸獎機會.摸獎規則如下:
獎盒中放有除顏色不同外其余完全相同的4個球(紅、黃、黑、白).顧客不放回的每次摸出1個球,若摸到黑球則摸獎停止,否則就繼續摸球.按規定摸到紅球獎勵20元,摸到白球或黃球獎勵10元,摸到黑球不獎勵.
(1)求1名顧客摸球2次摸獎停止的概率;
(2)記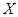 為1名顧客摸獎獲得的獎金數額,求隨機變量
為1名顧客摸獎獲得的獎金數額,求隨機變量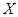 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設每個工作日甲、乙、丙、丁4人需使用某種設備的概率分別為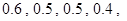 各人是否需使用設備相互獨立.
各人是否需使用設備相互獨立.
(1)求同一工作日至少3人需使用設備的概率;
(2)X表示同一工作日需使用設備的人數,求X的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某城市隨機抽取一年(365天)內100天的空氣質量指數API的監測數據,結果統計如下:
| API | 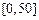 | 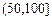 | 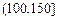 | 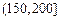 | 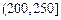 | 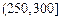 | 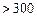 |
| 空氣質量 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天數 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
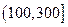 對企業造成經濟損失成直線模型(當API為150時造成的 經濟損失為500元,當API為200時,造成的經濟損失為700元);當API大于300時造成的 經濟損失為2000元;
對企業造成經濟損失成直線模型(當API為150時造成的 經濟損失為500元,當API為200時,造成的經濟損失為700元);當API大于300時造成的 經濟損失為2000元;
|
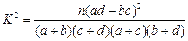
| | 非重度污染 | 重度污染 | 合計 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合計 | | | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某算法的程序框圖如圖所示,其中輸入的變量x在1,2,3,…,24這24個整數中等可能隨機產生.
(1)分別求出按程序框圖正確編程運行時輸出y的值為i的概率Pi(i=1,2,3);
(2)甲、乙兩同學依據自己對程序框圖的理解,各自編寫程序重復運行n次后,統計記錄了輸出y的值為i(i=1,2,3)的頻數.以下是甲、乙所作頻數統計表的部分數據.
甲的頻數統計表(部分)
| 運行次數n | 輸出y的值 為1的頻數 | 輸出y的值 為2的頻數 | 輸出y的值 為3的頻數 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2 100 | 1 027 | 376 | 697 |
| 運行次數n | 輸出y的值 為1的頻數 | 輸出y的值 為2的頻數 | 輸出y的值 為3的頻數 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2 100 | 1 051 | 696 | 353 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在某校趣味運動會的頒獎儀式上,為了活躍氣氛,大會組委會決定在頒獎過程中進行抽獎活動,用分層抽樣的方法從參加頒獎儀式的高一、高二、高三代表隊中抽取20人前排就座,其中高二代表隊有6人.
(1)把在前排就座的高二代表隊6人分別記為a,b,c,d,e,f,現從中隨機抽取2人上臺抽獎,求a和b至少有一人上臺抽獎的概率;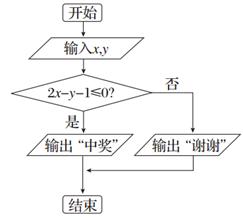
(2)抽獎活動的規則是:代表通過操作按鍵使電腦自動產生兩個[0,1]之間的隨機數x,y,并按如圖所示的程序框圖執行.若電腦顯示“中獎”,則該代表中獎;若電腦顯示“謝謝”,則不中獎.求該代表中獎的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com