【題目】下列四個結論： ①函數 
的值域是（0，+∞）；
②直線2x+ay﹣1=0與直線（a﹣1）x﹣ay﹣1=0平行，則a=﹣1；
③過點A（1，2）且在坐標軸上的截距相等的直線的方程為x+y=3；
④若圓柱的底面直徑與高都等于球的直徑，則圓柱的側面積等于球的表面積．
其中正確的結論序號為 ．
科目：高中數學 來源： 題型：
【題目】從雙曲線 
=1（a＞0，b＞0）的左焦點F引圓x2+y2=a2的切線，切點為T，延長FT交雙曲線右支于點P，若M為線段FP的中點，O為坐標原點，則|MO|﹣|MT|與b﹣a的大小關系為（ ）
A.|MO|﹣|MT|＞b﹣a
B.|MO|﹣|MT|=b﹣a
C.|MP|﹣|MT|＜b﹣a
D.不確定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=sin（ωx+φ）（ω＞0，|φ|＜ 
）的部分圖象如圖所示，則y=f（x）的圖象可由y=cos2x圖象（ ）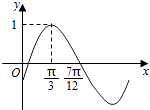 
A.向右平移 
個長度單位
B.向左平移 個長度單位
C.向右平移 
個長度單位
D.向左平移 個長度單位
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在多面體ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AD=AC，AB= 
DE，F是CD的中點． 
（1）求證：AF∥平面BCE；
（2）求證：平面BCE⊥平面CDE．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】假設關于某設備的使用年限x和所支出的維修費用y（萬元），有如下的統計資料：
x | 1 | 2 | 3 | 4 | 5 |
y | 5 | 6 | 7 | 8 | 10 |
由資料可知y對x呈線性相關關系，且線性回歸方程為 
，請估計使用年限為20年時，維修費用約為（ ）
A.26.2
B.27
C.27.6
D.28.2
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓兩焦點 
，并且經過點 
．
（1）求橢圓的方程；
（2）若過點A（0，2）的直線l與橢圓交于不同的兩點M、N（M在A、N之間），試求△OAM與△OAN面積之比的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓W： 
，過原點O作直線l1交橢圓W于A，B兩點，P為橢圓上異于A，B的動點，連接PA，PB，設直線PA，PB的斜率分別為k1 ， k2（k1 ， k2≠0），過O作直線PA，PB的平行線l2 ， l3 ， 分別交橢圓W于C，D和E，F．
（1）若A，B分別為橢圓W的左、右頂點，是否存在點P，使∠APB=90°？說明理由．
（2）求k1k2的值；
（3）求|CD|2+|EF|2的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知指數函數y=g（x）滿足：g（3）=8，定義域為R的函數f（x）= 
是奇函數．
（1）確定y=g（x），y=f（x）的解析式；
（2）若h（x）=f（x）+a在（﹣1，1）上有零點，求a的取值范圍；
（3）若對任意的t∈（﹣4，4），不等式f（6t﹣3）+f（t2﹣k）＜0恒成立，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某電視臺綜藝節目舉辦的挑戰主持人大賽上，七位評委為某選手打出的分數的莖葉統計圖，去掉一個最高分和一個最低分后，所剩數據的平均數和方差分別為（ ） 
A.84，4.84
B.84，1.6
C.85，4
D.85，1.6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
