
【題目】設函數![]() ,
,![]() ,
,![]() ,其中
,其中![]() 是
是![]() 的導函數.
的導函數.
(1)若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)設![]() ,比較
,比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
科目:高中數學 來源: 題型:
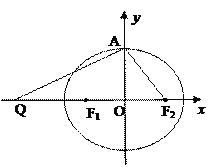
【題目】如圖,設橢圓![]() 的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且
的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且![]() 0,若過 A,Q,F2三點的圓恰好與直線
0,若過 A,Q,F2三點的圓恰好與直線![]() 相切,過定點 M(0,2)的直線
相切,過定點 M(0,2)的直線![]() 與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線
與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線![]() 的斜率
的斜率![]() ,在x軸上是否存在點P(
,在x軸上是否存在點P(![]() ,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出
,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數
的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數![]() 滿足
滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程。
已知曲線C![]() :
:![]() (t為參數), C
(t為參數), C![]() :
:![]() (
(![]() 為參數)。
為參數)。
(1)化C![]() ,C
,C![]() 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)若C![]() 上的點P對應的參數為
上的點P對應的參數為![]() ,Q為C
,Q為C![]() 上的動點,求
上的動點,求![]() 中點
中點![]() 到直線
到直線
![]() (t為參數)距離的最小值。
(t為參數)距離的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線![]() 的方程為
的方程為![]() ,以極點為原點,極軸所在直線為
,以極點為原點,極軸所在直線為![]() 軸建立直角坐標,直線
軸建立直角坐標,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),
為參數),![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設點![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比數列,求
成等比數列,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著現代社會的發展,我國對于環境保護越來越重視,企業的環保意識也越來越強.現某大型企業為此建立了5套環境監測系統,并制定如下方案:每年企業的環境監測費用預算定為1200萬元,日常全天候開啟3套環境監測系統,若至少有2套系統監測出排放超標,則立即檢查污染源處理系統;若有且只有1套系統監測出排放超標,則立即同時啟動另外2套系統進行1小時的監測,且后啟動的這2套監測系統中只要有1套系統監測出排放超標,也立即檢查污染源處理系統.設每個時間段(以1小時為計量單位)被每套系統監測出排放超標的概率均為![]() ,且各個時間段每套系統監測出排放超標情況相互獨立.
,且各個時間段每套系統監測出排放超標情況相互獨立.
(1)當![]() 時,求某個時間段需要檢查污染源處理系統的概率;
時,求某個時間段需要檢查污染源處理系統的概率;
(2)若每套環境監測系統運行成本為300元/小時(不啟動則不產生運行費用),除運行費用外,所有的環境監測系統每年的維修和保養費用需要100萬元.現以此方案實施,問該企業的環境監測費用是否會超過預算(全年按9000小時計算)?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站推出了關于生態文明建設進展情況的調查,大量的統計數據表明,參與調查者中關注此問題的約占80%.現從參與調查的人群中隨機選出![]() 人,并將這
人,并將這![]() 人按年齡分組:第1組
人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4 組
,第4 組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示
,得到的頻率分布直方圖如圖所示
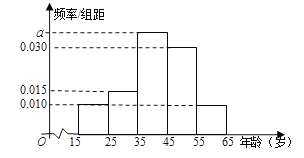
(1) 求![]() 的值
的值
(2)現在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行問卷調查,求在第1組已被抽到
人進行問卷調查,求在第1組已被抽到![]() 人的前提下,第3組被抽到
人的前提下,第3組被抽到![]() 人的概率;
人的概率;
(3)若從所有參與調查的人中任意選出![]() 人,記關注“生態文明”的人數為
人,記關注“生態文明”的人數為![]() ,求
,求![]() 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,兩種坐標系中取相同的長度單位.已知直線l的參數方程為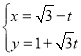 (t為參數),曲線C的極坐標方程為ρ=4sin(θ+
(t為參數),曲線C的極坐標方程為ρ=4sin(θ+![]() ).
).
(1)求直線l的普通方程與曲線C的直角坐標方程;
(2)若直線l與曲線C交于M,N兩點,求△MON的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產的產品中分正品與次品,正品重100克,次品重110 克.現有5袋產品(每袋裝有10個產品),已知其中有且只有一袋次品(10個產品均為次品),如果將5袋產品以1-5編號,第![]() 袋取出
袋取出![]() 個產品(
個產品(![]() =1,2,3,4,5),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量
=1,2,3,4,5),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量![]() ,若次品所在的袋子的編號是2,此時的重量
,若次品所在的袋子的編號是2,此時的重量![]() =__________克;若次品所在袋子的編號是
=__________克;若次品所在袋子的編號是![]() ,此時的重量
,此時的重量![]() =_________克.
=_________克.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com