
設(shè) 分別為橢圓
分別為橢圓 的左、右頂點(diǎn),橢圓長(zhǎng)半軸的長(zhǎng)等于焦距,且
的左、右頂點(diǎn),橢圓長(zhǎng)半軸的長(zhǎng)等于焦距,且 為它的右準(zhǔn)線.
為它的右準(zhǔn)線.
(Ⅰ)求橢圓的方程;
(Ⅱ)設(shè) 為右準(zhǔn)線上不同于點(diǎn)(4,0)的任意一點(diǎn),若直線
為右準(zhǔn)線上不同于點(diǎn)(4,0)的任意一點(diǎn),若直線 分別與橢圓相交于異于
分別與橢圓相交于異于 的點(diǎn)
的點(diǎn) ,證明點(diǎn)
,證明點(diǎn) 在以
在以 為直徑的圓內(nèi).
為直徑的圓內(nèi).
(此題不要求在答題卡上畫圖)

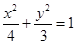
【解析】(I)依題意得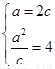 解得
解得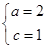 從而b=
從而b=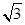 ,………………………………………3分
,………………………………………3分
故橢圓方程為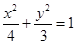 .……………………………………………………………………4分
.……………………………………………………………………4分
(II)解法1:由(I)得A(-2,0),B(2,0),設(shè)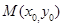 .
.
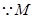 點(diǎn)在橢圓上,
點(diǎn)在橢圓上, .……………………………………………………… 5分
.……………………………………………………… 5分
又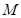 點(diǎn)異于頂點(diǎn)
點(diǎn)異于頂點(diǎn)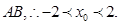
由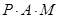 三點(diǎn)共線可得
三點(diǎn)共線可得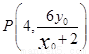 ,…………………………………………………………………6分
,…………………………………………………………………6分
從而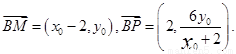 .……………………………………………………………7分
.……………………………………………………………7分
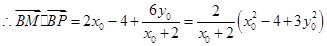 ,………………………………………………10分
,………………………………………………10分
將①式代入②式化簡(jiǎn)得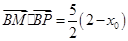 .…………………………………………………………12分
.…………………………………………………………12分
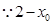 >0,
>0,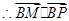 >0.于是
>0.于是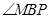 為銳角,從而
為銳角,從而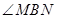 為鈍角,
為鈍角,
故點(diǎn)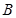 在以
在以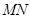 為直徑的圓內(nèi).………………………………………………………………………. 14分
為直徑的圓內(nèi).………………………………………………………………………. 14分
解法2:由(Ⅰ)得A(-2,0),B(2,0).設(shè)P(4,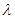 )(
)(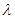
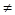 0),M(
0),M(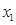 ,
,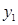 ),N(
),N(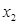 ,
,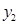 ),則直線AP的方程為
),則直線AP的方程為 ,直線BP的方程為
,直線BP的方程為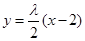 .…………………………….. 6分
.…………………………….. 6分
 點(diǎn)M、N分別在直線AP、BP上,
點(diǎn)M、N分別在直線AP、BP上,
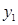 =
= (
(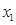 +2),
+2),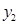 =
=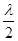 (
(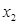 -2).從而
-2).從而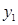
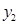 =
=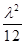 (
(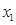 +2)(
+2)(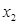 -2).③
-2).③
聯(lián)立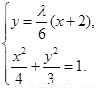 消去y得(27+
消去y得(27+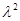 )
)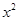 +4
+4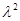 x+4(
x+4(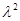 -27)=0………………8分
-27)=0………………8分
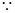
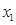 ,-2是方程得兩根,
,-2是方程得兩根,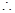 (-2).
(-2). ,即
,即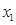 =
=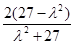 . ④
. ④
又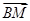 .
.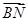 =(
=(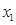 -2,
-2, 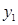 ).(
).(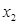 -2,
-2,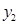 )=(
)=(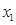 -2)(
-2)(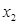 -2)+
-2)+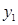
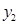 . ⑤………9分
. ⑤………9分
于是由③、④式代入⑤式化簡(jiǎn)可得
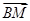 .
.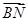 =
=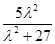 (
(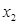 -2)………………………………………………………… 12分
-2)………………………………………………………… 12分
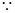 N點(diǎn)在橢圓上,且異于頂點(diǎn)A、B,
N點(diǎn)在橢圓上,且異于頂點(diǎn)A、B,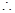
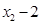 <0.
<0.
又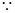
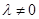 ,
,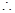
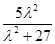 > 0, 從而
> 0, 從而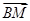 .
.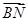 <0.
<0.
故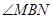
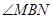 為鈍角,即點(diǎn)B在以MN為直徑的圓內(nèi)………………………………14分
為鈍角,即點(diǎn)B在以MN為直徑的圓內(nèi)………………………………14分
解法3:由(Ⅰ)得A(-2,0),B(2,0).設(shè)M(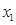 ,
,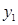 ),N(
),N(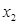 ,
,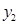 ),則-2<
),則-2<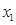 <2
, -2<
<2
, -2<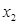 <2.又MN的中點(diǎn)Q的坐標(biāo)為(
<2.又MN的中點(diǎn)Q的坐標(biāo)為(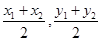 ),………………………………………5分
),………………………………………5分
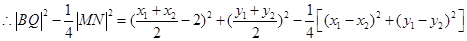
化簡(jiǎn)得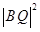 -
-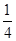
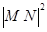 =(
=(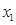 -2)(
-2)(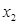 -2)+
-2)+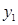
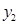 .
⑥………………8分
.
⑥………………8分
直線AP的方程為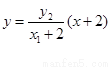 ,直線BP的方程為
,直線BP的方程為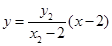 ………………10分
………………10分
 點(diǎn)P在準(zhǔn)線x=4上,
點(diǎn)P在準(zhǔn)線x=4上,
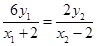 ,即
,即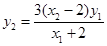 .
⑦
.
⑦
又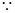 M點(diǎn)在橢圓上,
M點(diǎn)在橢圓上,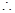
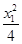 +
+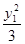 =1,即
=1,即 ⑧……… 12分
⑧……… 12分
于是將⑦、⑧式化簡(jiǎn)可得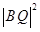 -
-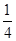
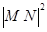 =
=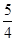
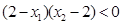 .
.
從而B在以MN為直徑的圓內(nèi)………………………………………………………………… 14分



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2014屆浙江省高二下學(xué)期期中文科數(shù)學(xué)試卷(解析版) 題型:選擇題
設(shè) 分別為橢圓
分別為橢圓 的左、右焦點(diǎn),點(diǎn)A,B在橢圓上,若
的左、右焦點(diǎn),點(diǎn)A,B在橢圓上,若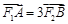 ,
,
則點(diǎn)A的坐標(biāo)是( )
A. B.
B. C.
C.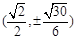 D.
D.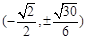
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年湖北省武漢市武昌區(qū)高三五月調(diào)研理科數(shù)學(xué)試卷(解析版) 題型:選擇題
設(shè) 分別為橢圓
分別為橢圓 的左、右頂點(diǎn),若在橢圓上存在異于
的左、右頂點(diǎn),若在橢圓上存在異于 的點(diǎn)
的點(diǎn) ,使得
,使得 ,其中
,其中 為坐標(biāo)原點(diǎn),則橢圓的離心率
為坐標(biāo)原點(diǎn),則橢圓的離心率 的取值范圍是
的取值范圍是
A.
 B.
B. C.
C.
 D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年江西省高三第四次月考理科數(shù)學(xué)試卷 題型:解答題
設(shè) ,
, 分別為橢圓
分別為橢圓
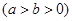 的左、右焦點(diǎn),過
的左、右焦點(diǎn),過 的直線
的直線 與橢圓
與橢圓 相交于
相交于 ,
, 兩點(diǎn),直線
兩點(diǎn),直線 的傾斜角為
的傾斜角為 ,
, 到直線
到直線 的距離為
的距離為 .
.
(1)求橢圓 的焦距;
的焦距;
(2)如果 ,求橢圓
,求橢圓 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012年湖南省高二上(12月)月考試題數(shù)學(xué) 題型:填空題
設(shè) 分別為橢圓
分別為橢圓 的左、右焦點(diǎn),點(diǎn)
的左、右焦點(diǎn),點(diǎn) 在橢圓上,若
在橢圓上,若 ;則點(diǎn)
;則點(diǎn) 的坐標(biāo)是
______.
的坐標(biāo)是
______.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com