【題目】設(shè)
數(shù)列
的前
項和，對任意
，都有
（
為常數(shù)）．
（1）當(dāng)
時，求；
（2）當(dāng)
時，
（ⅰ）求證：數(shù)列是等差數(shù)列；
（ⅱ）若對任意
，必存在
使得
，已知
，且
，求數(shù)列的通項公式．
【答案】(1) 
.
(2) （ⅰ）證明見解析；（ⅱ）
.
【解析】
（1）利用項和公式求出
是以1為首項，3為公比的等比數(shù)列，再求
.(2) （ⅰ）證明
即證數(shù)列
是等差數(shù)列. （ⅱ）先求得
，所以
或
，再求
，再檢驗
即得數(shù)列的通項公式.
（1）當(dāng)
，
，
時，
．①
當(dāng)
時，
，所以．
當(dāng)
時，
．②
①－②得：
．因為，所以
，所以
，
所以是以1為首項，3為公比的等比數(shù)列，
所以
．
（2）（ⅰ）當(dāng)
，
，
時，
．③
當(dāng)時，
．④
③－④得：
，⑤
所以
．⑥
⑤－⑥得：
．
因為，所以 即
，
所以是等差數(shù)列．
（ⅱ）因為
，所以
．
因為
，所以
，所以
．
因為
，所以
．又因為
，
所以，所以或．
當(dāng)時，
，
，
，
所以
不符合題意．
當(dāng)時，，
，
所以
滿足題意．
所以．
天天向上一本好卷系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】祖暅?zhǔn)悄媳背瘯r代的偉大科學(xué)家，5世紀(jì)末提出體積計算原理，即祖暅原理: “冪勢既同，則積不容異”.意思是:夾在兩個乎行平面之間的兩個幾何體，被平行于這兩個平面的任何一個平面所截，如果截面面積都相等，那么這兩個幾何體的體積一定相等.現(xiàn)將曲線
繞
軸旋轉(zhuǎn)一周得到的幾何體叫做橢球體，記為
，幾何體
的三視圖如圖所示.根據(jù)祖暅原理通過考察可以得到的體積，則的體積為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知奇函數(shù)
的定義域為[-1,1]，當(dāng)
時，
。
（1）求函數(shù)在
上的值域；
（2）若
時，函數(shù)
的最小值為-2，求實數(shù)λ的值。
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為建設(shè)美麗鄉(xiāng)村，政府欲將一塊長12百米，寬5百米的矩形空地ABCD建成生態(tài)休閑園，園區(qū)內(nèi)有一景觀湖EFG（圖中陰影部分）．以AB所在直線為x軸，AB的垂直平分線為y軸，建立平面直角坐標(biāo)系xOy（如圖所示）．景觀湖的邊界曲線符合函數(shù)
模型．園區(qū)服務(wù)中心P在x軸正半軸上，PO＝
百米．
（1）若在點O和景觀湖邊界曲線上一點M之間修建一條休閑長廊OM，求OM的最短長度；
（2）若在線段DE上設(shè)置一園區(qū)出口Q，試確定Q的位置，使通道直線段PQ最短．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】甲乙兩人玩一種游戲，每次由甲、乙各出1到5根手指，若和為偶數(shù)算甲贏，否則算乙贏.
（1）若以
表示和為6的事件，求
；
（2）現(xiàn)連玩三次，若以
表示甲至少贏一次的事件，
表示乙至少贏兩次的事件，試問
與
是否為互斥事件？為什么？
（3）這種游戲規(guī)則公平嗎？試說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
.
（1）當(dāng)
時，求函數(shù)
的單調(diào)區(qū)間和極值；
（2）若對于任意
，都有
成立，求實數(shù)
的取值范圍；
（3）若
，且
，證明：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
．
（1）若
在
處取得極值，求
的值；
（2）設(shè)
，試討論函數(shù)
的單調(diào)性；
（3）當(dāng)
時，若存在正實數(shù)
滿足
，求證：
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)
是由
個有序?qū)崝?shù)構(gòu)成的一個數(shù)組，記作：
.其中
稱為數(shù)組的“元”，
為
的下標(biāo).如果數(shù)組
中的每個“元”都來自數(shù)組中不同下標(biāo)的“元”則稱為的子數(shù)組.定義兩個數(shù)組
，
的關(guān)系數(shù)為
.
（1）若
，
，設(shè)是
的含有兩個“元”的子數(shù)組，求
的最大值及此時的數(shù)組；
（2）若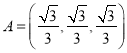
，
，且
，為的含有三個“元”的子數(shù)組，求的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）討論函數(shù)
的單調(diào)區(qū)間；
（2）若函數(shù)在
處取得極值，對
恒成立，求實數(shù)
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com