【題目】函數
在
內有兩個零點，則實數
的取值范圍是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
設
，則函數等價為
，條件轉化為
，進而轉化為
與
有兩個交點，利用函數的單調性和導數的幾何意義，結合絕對值，合理分類討論，即可求解，得到答案.
由題意，函數
，
設，則
，
因為
，所以
，
則函數
等價于
，
即等價為在上有兩個零點，
即在有兩個根，
設
，則
，即函數
是奇函數，
則
，即函數在上是增函數，
且
，
當
，若
時，則函數只有一個零點，不滿足條件；
若
時，則
，
設過原點的直線與相切，切點為
，
由，則
，
則切線方程為
，
切線過原點，則
，即
，
則
，
當
，即切點為
，此時切線的斜率為
，
若
，則
，此時切線
與
相切，只有一個交點，不滿足題意.
當直線過點
時，
，
此時直線
，
要使得
與由兩個交點，則
，
當
時，
時，
，
由
，得
，當直線過點
時，
，
要使得與由兩個交點，則
，
綜上或，
即實數
的取值范圍是
，
故選D.
科目：高中數學 來源： 題型：
【題目】已知函數
（a，
）.
（1）若
，且
在
內有且只有一個零點，求a的值；
（2）若
，且有三個不同零點，問是否存在實數a使得這三個零點成等差數列？若存在，求出a的值，若不存在，請說明理由；
（3）若
，
，試討論是否存在
，使得
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，在梯形ABCD中，AB//CD，AB=3，CD=6，過A，B分別作CD的垂線，垂足分別為E，F，已知DE=1，AE=3，將梯形ABCD沿AE，BF同側折起，使得平面ADE⊥平面ABFE，平面ADE∥平面BCF，得到圖2.
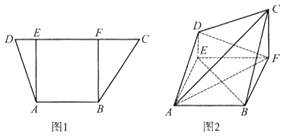
（1）證明：BE//平面ACD；
（2）求三棱錐C﹣AED的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】移動支付（支付寶及微信支付）已經漸漸成為人們購物消費的一種支付方式，為調查市民使用移動支付的年齡結構，隨機對100位市民做問卷調查得到
列聯表如下：
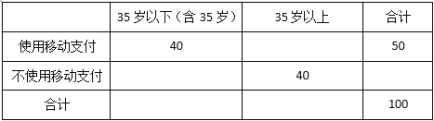
（1）將上列聯表補充完整，并請說明在犯錯誤的概率不超過0．10的前提下，認為支付方式與年齡是否有關？
（2）在使用移動支付的人群中采用分層抽樣的方式抽取10人做進一步的問卷調查，從這10人隨機中選出3人頒發參與獎勵，設年齡都低于35歲（含35歲）的人數為
，求的分布列及期望．
（參考公式：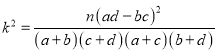
（其中
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
