Question

已知（c>0），（n, n）（n∈R）, 的最小值為1，若動點P同時滿足下列三個條件：①，②（其中）；③動點P的軌跡C經過點B（0,－1）。

（1）求c值；  （2）求曲線C的方程；（3）方向向量為的直線l與曲線C交于不同兩點M、N，若，求k的取值范圍。

Answer 1

(1) ,(2) 曲線C的方程為：,

(3) 的取值范圍是。

解析:

（1）法一，∵

                 

當時，                           

法二，由可知點G在直線y=x上

∴|FG|的最小值為點F到直線y=x的距離，即       （）

（2）由知 又

又（）∴∴點P在以F為焦點，為準線的橢圓上

設P(x,y)，則∵動點P的軌跡C經過點B(0,-1)且

∴從而b=1  ∴曲線C的方程為：

（3）設直線的方程為

由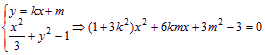     

∵與曲線C交于不同兩點，∴，即①

設的中點由則有BR⊥MN

∵K_MN=K_L=K∴（11分）由韋達定理有

∴∴MN的中點R₀坐標為（12分）又B（0，-1）

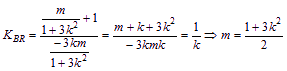∴    ②

由①②聯立可得

即∴為R上的減函數

（3分）志求閉區間為[-1，1]

（2）（5分）（或∵）∴在R不可能恒為正式恒為負）

      

        

∴在R上不是單調函數，故不是閉函數

（3）在（0，）上是增函數

設[]（0，∞），  

即方程有兩個不相等的正根（12分）

于是

故的取值范圍是