
(本小題10分)已知函數(shù)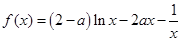 .
.
(1)試討論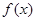 的單調(diào)性;
的單調(diào)性;
(2)如果當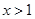 時,
時,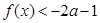 ,求實數(shù)
,求實數(shù)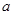 的取值范圍;
的取值范圍;
(3)記函數(shù)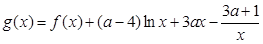 ,若
,若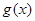 在區(qū)間
在區(qū)間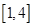 上不單調(diào), 求實數(shù)
上不單調(diào), 求實數(shù)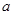 的取值范圍.
的取值范圍.
解:(1)①若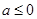 ,則
,則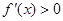 ,所以
,所以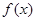 在
在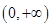 上單調(diào)遞增
上單調(diào)遞增
②若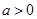 ,則由
,則由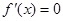 ,得
,得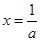 ,且當
,且當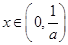 時,
時,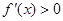 ,當
,當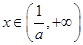 時,
時,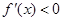 ,所以
,所以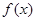 在
在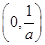 上單調(diào)遞增,在
上單調(diào)遞增,在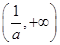 上單調(diào)遞減;
上單調(diào)遞減;
(2)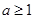 ;(3)
;(3)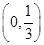 .
.
【解析】本試題主要是考查了導數(shù)在研究函數(shù)中的運用。解決不等式的恒成立問題,和函數(shù)的單調(diào)性的逆向運用的綜合試題。
(1)首先求解導數(shù),根據(jù)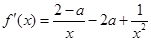
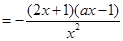 的分子為含有參數(shù)的二次函數(shù),那么結(jié)合二次不等式進行分情況討論得到單調(diào)區(qū)間。
的分子為含有參數(shù)的二次函數(shù),那么結(jié)合二次不等式進行分情況討論得到單調(diào)區(qū)間。
(2)利用當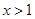 時,
時,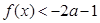 ,結(jié)合上一問的單調(diào)性,確定最值,解得a的范圍。
,結(jié)合上一問的單調(diào)性,確定最值,解得a的范圍。
(3)利用等價轉(zhuǎn)化思想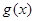 在區(qū)間
在區(qū)間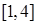 上不單調(diào)
上不單調(diào)
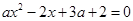
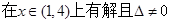 ,然后分離變量求解參數(shù)的取值范圍。
,然后分離變量求解參數(shù)的取值范圍。
解:(1)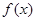 的定義域為
的定義域為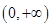 ,
,
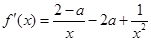
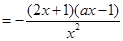 ……2分
……2分
①若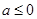 ,則
,則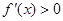 ,所以
,所以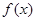 在
在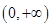 上單調(diào)遞增
上單調(diào)遞增
②若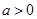 ,則由
,則由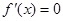 ,得
,得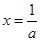 ,且當
,且當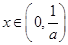 時,
時,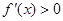 ,當
,當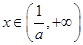 時,
時,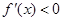 ,所以
,所以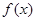 在
在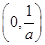 上單調(diào)遞增,在
上單調(diào)遞增,在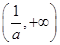 上單調(diào)遞減;
……4分
上單調(diào)遞減;
……4分
(2)由(1)知:
①若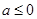 時,
時,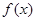 在
在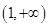 上單調(diào)遞增,所以
上單調(diào)遞增,所以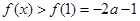 ,不合;
,不合;
②若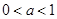 時,
時,
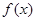 在
在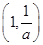 上單調(diào)遞增,在
上單調(diào)遞增,在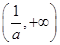 上單調(diào)遞減;所以
上單調(diào)遞減;所以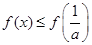 ,又
,又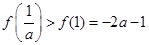 ,不合;
,不合;
③若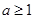 時,
時,
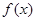 在
在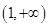 上單調(diào)遞減;所以
上單調(diào)遞減;所以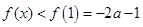 ,
,
綜上所述,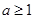 …………7分
…………7分
(3)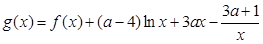
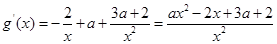
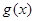 在區(qū)間
在區(qū)間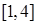 上不單調(diào)
上不單調(diào)
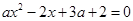
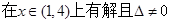
變量分離得,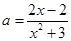
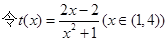 ,求得
,求得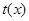 的值域為
的值域為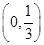
 ……10分
……10分


 每課必練系列答案
每課必練系列答案科目:高中數(shù)學 來源:2010年黑龍江省哈六中高一下學期期中考試數(shù)學試題 題型:解答題
(本小題10分)
已知等差數(shù)列 ,
,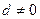 ,
,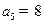 ,且項
,且項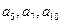 分別是某一等比數(shù)列
分別是某一等比數(shù)列 中的第
中的第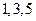 項,(1)求數(shù)列
項,(1)求數(shù)列 的第12項; (2)求數(shù)列
的第12項; (2)求數(shù)列 的第
的第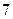 項。
項。
查看答案和解析>>
科目:高中數(shù)學 來源:2011年山東省濟南外國語學校高一入學檢測數(shù)學試卷 題型:解答題
(本小題10分)
已知直線
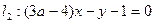 且
且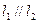 ,求以N(1,1)為圓心,并且與
,求以N(1,1)為圓心,并且與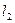 相切的圓的方程.
相切的圓的方程.
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年遼寧沈陽二中等重點中學協(xié)作體高三領(lǐng)航高考預(yù)測(六)理數(shù)學卷(解析版) 題型:解答題
(本小題10分)已知C點在⊙O直徑BE的延長線上,CA切⊙O于A 點,CD是∠ACB的平分線且交AE于點F,交AB于點D.
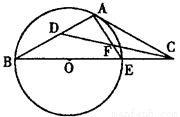
(1)求∠ADF的度數(shù);
(2)若AB=AC,求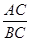 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源:2014屆吉林省高一下學期期末理科數(shù)學試卷(解析版) 題型:解答題
(本小題10分)已知圓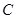 經(jīng)過
經(jīng)過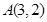 、
、 兩點,且圓心在直線
兩點,且圓心在直線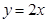 上.
上.
(1) 求圓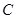 的方程;
的方程;
(2) 若直線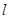 經(jīng)過點
經(jīng)過點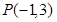 且與圓
且與圓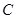 相切,求直線
相切,求直線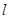 的方程.
的方程.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com