【題目】某電子科技公司由于產品采用最新技術，銷售額不斷增長，最近
個季度的銷售額數據統計如下表（其中
表示
年第一季度，以此類推）：
季度 |
|
|
|
|
|
季度編號x |
|
|
|
|
|
銷售額y（百萬元） |
|
|
|
|
|
（1）公司市場部從中任選
個季度的數據進行對比分析，求這個季度的銷售額都超過
千萬元的概率；
（2）求
關于
的線性回歸方程，并預測該公司
的銷售額.
附：線性回歸方程：
其中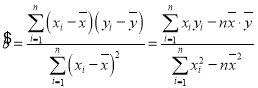
，
參考數據：
.
【答案】（1）
；（2）
關于
的線性回歸方程為
，預測該公司
的銷售額為
百萬元.
【解析】
（1）列舉出所有的基本事件，并確定事件“這
個季度的銷售額都超過
千萬元”然后利用古典概型的概率公式可計算出所求事件的概率；
（2）計算出
和
的值，然后將表格中的數據代入最小二乘法公式，計算出
和
的值，可得出關于的線性回歸方程，然后將
代入回歸直線方程即可得出該公司的銷售額的估計值.
（1）從
個季度的數據中任選個季度，這個季度的銷售額有
種情況：
、
、
、
、
、
、
、
、
、
設“這個季度的銷售額都超過千萬元”為事件
，事件包含、、，
種情況，所以
；
（2）
，
，
，
.
所以關于的線性回歸方程為，
令，得
（百萬元）
所以預測該公司的銷售額為百萬元．
備戰中考寒假系列答案科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]
在直角坐標系
中，曲線
的參數方程為
（
是參數），以坐標原點為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線的普通方程和曲線的直角坐標方程；
（2）設曲線經過伸縮變換
得到曲線
，
是曲線上任意一點，求點
到曲線的距離的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
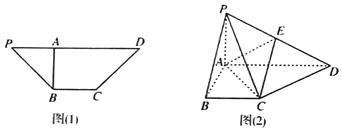
【題目】如圖
在四邊形PBCD中，
，
，
，
，
，沿AB把三角形PAB折起，使P，D兩點的距離為10，得到如圖
所示圖形．
Ⅰ
求證：平面
平面PAC；
Ⅱ若點E是PD的中點，求三棱錐
的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
（
）過點
，短軸一個端點到右焦點的距離為2．
（1）求橢圓C的方程；
（2）設過定點
的直線1與橢圓交于不同的兩點A，B，若坐標原點O在以線段AB為直徑的圓上，求直線l的斜率k．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種“籠具”由內，外兩層組成，無下底面，內層和外層分別是一個圓錐和圓柱，其中圓柱與圓錐的底面周長相等，圓柱有上底面，制作時需要將圓錐的頂端剪去，剪去部分和接頭忽略不計，已知圓柱的底面周長為
，高為
，圓錐的母線長為
.
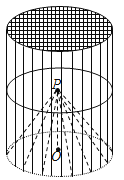
（1）求這種“籠具”的體積（結果精確到0.1
）；
（2）現要使用一種紗網材料制作50個“籠具”，該材料的造價為每平方米8元，共需多少元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一橢圓形溜冰場，長軸長100米，短軸長為60米，現要在這溜冰場上劃定一個各頂點都在溜冰場邊界上的矩形區域，且使這個區域的面積最大，應把這個矩形的頂點定位在何處？并求出此矩形的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
