
(08年四川卷理)設橢圓![]() 的左、右焦點分別是
的左、右焦點分別是![]() 、
、![]() ,離心率
,離心率![]() ,右準線
,右準線![]() 上的兩動點
上的兩動點![]() 、
、![]() ,且
,且![]() .
.
(Ⅰ)若![]() ,求
,求![]() 、
、![]() 的值;
的值;
(Ⅱ)當![]() 最小時,求證
最小時,求證![]() 與
與![]() 共線.
共線.

解析:數列和解幾位列倒數第三和第二,意料之中.開始擠牙膏吧.
(Ⅰ)由已知,![]() ,
,![]() .由
.由![]() ,
,![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() :
:![]() ,
,![]() ,
,![]() .
.
延長![]() 交
交![]() 于
于![]() ,記右準線
,記右準線![]() 交
交![]() 軸于
軸于![]() .
.
∵![]() ,∴
,∴![]() .
.![]()
由平幾知識易證![]() ≌
≌![]()
∴![]() ,
,![]()
即![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
(Ⅰ)另解:∵![]() ,∴
,∴![]() ,
,![]() .
.
又![]()
聯立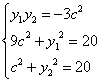 ,消去
,消去![]() 、
、![]() 得:
得:![]() ,
,
整理得:![]() ,
,![]() .解得
.解得![]() .但解此方程組要考倒不少人.
.但解此方程組要考倒不少人.
(Ⅱ)∵![]() ,∴
,∴![]() .
.
![]() .
.
當且僅當![]() 或
或![]() 時,取等號.此時
時,取等號.此時![]() 取最小值
取最小值![]() .
.
此時![]() .
.
∴![]() 與
與![]() 共線.
共線.
(Ⅱ)另解:∵![]() ,∴
,∴![]() ,
,![]() .
.
設![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .
.
由![]() ,由
,由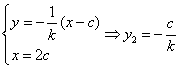
![]() .當且僅當
.當且僅當![]() 即
即![]() ,
,![]() 時取等號.
時取等號.
即當![]() 最小時,
最小時,![]() ,
,
此時![]() .
.
∴![]() 與
與![]() 共線.
共線.
點評:本題第一問又用到了平面幾何.看來,與平面幾何有聯系的難題真是四川風格啊.注意平面幾何可與三角向量解幾沾邊,應加強對含平面幾何背景的試題的研究.本題好得好,出得活,出得妙!均值定理,放縮技巧,永恒的考點.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
(08年四川卷理)設進入某商場的每一位顧客購買甲商品的概率0.5,購買乙商品的概率為0.6,且顧客購買甲商品與購買乙商品相互獨立,每位顧客間購買商品也相互獨立.
(Ⅰ)求進入商場的1位顧客購買甲、乙兩種商品中的一種的概率;
(Ⅱ)求進入商場的1位顧客至少購買甲、乙兩種商品中的一種的概率;
(Ⅲ)設![]() 是進入商場的3位顧客至少購買甲、乙商品中一種的人數,求
是進入商場的3位顧客至少購買甲、乙商品中一種的人數,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com