
【題目】已知橢圓![]() 和圓
和圓![]() ,
,![]() 、
、![]() 為橢圓
為橢圓![]() 的左、右焦點,點
的左、右焦點,點![]() 在橢圓
在橢圓![]() 上,當直線
上,當直線![]() 與圓
與圓![]() 相切時,
相切時,![]() .
.
(I)求![]() 的方程;
的方程;
(Ⅱ)直線![]() 與橢圓
與橢圓![]() 和圓
和圓![]() 都相切,切點分別為
都相切,切點分別為![]() 、
、![]() ,求
,求![]() 面積的最大值.
面積的最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】2016年春節期間全國流行在微信群里發搶紅包,現假設某人將688元發成手氣紅包50個,產生的手氣紅包頻數分布表如下:
金額分組 |
|
|
|
|
|
|
頻 數 | 3 | 9 | 17 | 11 | 8 | 2 |
(1)求產生的手氣紅包的金額不小于9元的頻率;
(2)估計手氣紅包金額的平均數(同一組中的數據用該組區間的中點值作代表);
(3)在這50個紅包組成的樣本中,將頻率視為概率.
①若紅包金額在區間![]() 內為最佳運氣手,求搶得紅包的某人恰好是最佳運氣手的概率;
內為最佳運氣手,求搶得紅包的某人恰好是最佳運氣手的概率;
②隨機抽取手氣紅包金額在![]() 內的兩名幸運者,設其手氣金額分別為
內的兩名幸運者,設其手氣金額分別為![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
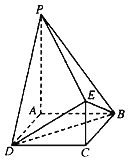
(1)證明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對數是簡化繁雜運算的產物.16世紀時,為了簡化數值計算,數學家希望將乘除法歸結為簡單的加減法.當時已經有數學家發現這在某些情況下是可以實現的.
比如,利用以下2的次冪的對應表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16與256;然后找出它們在第一行對應的數,即4與8,并求它們的和,即12;最后在第一行中找到12,讀出其對應的第二行中的數4096,這就是![]() 的值.
的值.
用類似的方法可以算出![]() 的值,首先,在第二行找到4096與128;然后找出它們在第一行對應的數,即12與7,并求它們的______;最后在第一行中找到______,讀出其對應的第二行中的數______,這就是
的值,首先,在第二行找到4096與128;然后找出它們在第一行對應的數,即12與7,并求它們的______;最后在第一行中找到______,讀出其對應的第二行中的數______,這就是![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 是坐標原點,橢圓
是坐標原點,橢圓![]() :
:![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,點
,點![]() 在橢圓上,若
在橢圓上,若![]() 的面積最大時
的面積最大時![]() 且最大面積為
且最大面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() :
:![]() 與橢圓
與橢圓![]() 在第一象限交于點
在第一象限交于點![]() ,點
,點![]() 是第四象限內的點且在橢圓
是第四象限內的點且在橢圓![]() 上,線段
上,線段![]() 被直線
被直線![]() 垂直平分,直線
垂直平分,直線![]() 與橢圓交于另一點
與橢圓交于另一點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學參加某個知識答題游戲節目,答題分兩輪,第一輪為“選題答題環節”第二輪為“輪流坐莊答題環節”.首先進行第一輪“選題答題環節”,答題規則是:每位同學各自從備選的5道不同題中隨機抽出3道題進行答題,答對一題加10分,答錯一題(不答視為答錯)減5分,已知甲能答對備選5道題中的每道題的概率都是![]() ,乙恰能答對備選5道題中的其中3道題;第一輪答題完畢后進行第二輪“輪流坐莊答題環節”,答題規則是:先確定一人坐莊答題,若答對,繼續答下一題…,直到答錯,則換人(換莊)答下一題…以此類推.例如若甲首先坐莊,則他答第1題,若答對繼續答第2題,如果第2題也答對,繼續答第3題,直到他答錯則換成乙坐莊開始答下一題,…直到乙答錯再換成甲坐莊答題,依次類推兩人共計答完20道題游戲結束,假設由第一輪答題得分期望高的同學在第二輪環節中最先開始作答,且記第
,乙恰能答對備選5道題中的其中3道題;第一輪答題完畢后進行第二輪“輪流坐莊答題環節”,答題規則是:先確定一人坐莊答題,若答對,繼續答下一題…,直到答錯,則換人(換莊)答下一題…以此類推.例如若甲首先坐莊,則他答第1題,若答對繼續答第2題,如果第2題也答對,繼續答第3題,直到他答錯則換成乙坐莊開始答下一題,…直到乙答錯再換成甲坐莊答題,依次類推兩人共計答完20道題游戲結束,假設由第一輪答題得分期望高的同學在第二輪環節中最先開始作答,且記第![]() 道題也由該同學(最先答題的同學)作答的概率為
道題也由該同學(最先答題的同學)作答的概率為![]() (
(![]() ),其中
),其中![]() ,已知供甲乙回答的20道題中,甲,乙兩人答對其中每道題的概率都是
,已知供甲乙回答的20道題中,甲,乙兩人答對其中每道題的概率都是![]() ,如果某位同學有機會答第
,如果某位同學有機會答第![]() 道題且回答正確則該同學加10分,答錯(不答視為答錯)則減5分,甲乙答題相互獨立;兩輪答題完畢總得分高者勝出.回答下列問題
道題且回答正確則該同學加10分,答錯(不答視為答錯)則減5分,甲乙答題相互獨立;兩輪答題完畢總得分高者勝出.回答下列問題
(1)請預測第二輪最先開始作答的是誰?并說明理由
(2)①求第二輪答題中![]() ,
,![]() ;
;
②求證![]() 為等比數列,并求
為等比數列,并求![]() (
(![]() )的表達式.
)的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校實行新課程改革,即除語、數、外三科為必考科目外,還要在理、化、生、史、地、政六科中選擇三科作為選考科目.已知某生的高考志愿為某大學環境科學專業,按照該大學上一年高考招生選考科目要求理、化必選,為該生安排課表(上午四節、下午四節,每門課每天至少一節),已知該生某天最后兩節為自習課,且數學不排下午第一節,語文、外語不相鄰(上午第四節和下午第一節不算相鄰),則該生該天課表有( ).
A.444種B.1776種C.1440種D.1560種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com