
【題目】設(shè)函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求證:
時(shí),求證:![]() ;
;
(2)當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見(jiàn)解析(2)![]()
【解析】
(1)當(dāng)![]() 時(shí),
時(shí),![]() ,不等式
,不等式![]() 化為
化為![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,利用導(dǎo)數(shù)求函數(shù)
,利用導(dǎo)數(shù)求函數(shù)![]() 的最小值,從而證明不等式成立;
的最小值,從而證明不等式成立;
(2)方法1:不等式化為![]() ,令
,令![]() ,利用導(dǎo)數(shù)判斷
,利用導(dǎo)數(shù)判斷![]() ,不等式化為
,不等式化為![]() ,記
,記![]() ,求出
,求出![]() 的最大值,即可得出
的最大值,即可得出![]() 的取值范圍.
的取值范圍.
方法2:討論![]() 時(shí),
時(shí),![]() ,求得
,求得![]() 的取值范圍,再證明
的取值范圍,再證明![]() 時(shí),
時(shí),![]() 在
在![]() 上
上![]() 恒成立.
恒成立.
(1)當(dāng)![]() 時(shí),
時(shí),![]() ,
,
要證明![]() ,即證明
,即證明![]() ;
;
記![]() ,則
,則![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當(dāng)![]() 時(shí),
時(shí),![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
所以![]() ,即
,即![]() ;
;
(2)方法1:![]() 即
即![]() ,
,
令![]() ,令
,令![]() ,得
,得![]() ;
;
所以![]() 在
在 上單調(diào)減,在
上單調(diào)減,在 單調(diào)增,
單調(diào)增,
則 ,
,
即![]() ,可化為
,可化為![]() ,
,
記![]() ,則
,則 ,且
,且![]() ;
;
再令![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
![]() ,
,
由(1)可知![]() ,
,![]() 時(shí)成立,
時(shí)成立,![]() ,
, ,
,
由此 ,
,![]() 在
在![]() 上單調(diào)增;
上單調(diào)增;
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)減;
上單調(diào)減;
因此![]() ,故
,故![]() ;
;
方法2:當(dāng)![]() 時(shí),
時(shí),![]() ,由此
,由此![]()
證明如下:當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上,
上,![]() 恒成立,
恒成立,
![]() ,同法1證明,
,同法1證明,![]() ,
,
![]() ;
;
所以![]() 在
在![]() 上,
上,![]() 恒成立,故
恒成立,故![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)求![]() 在
在![]() 上的單調(diào)性及極值;
上的單調(diào)性及極值;
(2)若![]() ,對(duì)任意的
,對(duì)任意的![]() ,不等式
,不等式![]() 都在
都在![]() 上有解,求實(shí)數(shù)
上有解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知f(x)是定義在R上的偶函數(shù),且x≤0時(shí), f(x)=-x+1
(1)求f(0),f(2);
(2)求函數(shù)f(x)的解析式;
(3)若f(a-1)<3,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在正方形![]() 中,
中,![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() .若將
.若將![]() ,
, ![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 兩點(diǎn)重合于點(diǎn)
兩點(diǎn)重合于點(diǎn)![]() ,如圖2.
,如圖2.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值
所成角的正弦值

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,且離心率為
,且離心率為![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)過(guò)![]() 作斜率分別為
作斜率分別為![]() 的兩條直線,分別交橢圓于點(diǎn)
的兩條直線,分別交橢圓于點(diǎn)![]() ,且
,且![]() ,證明:直線
,證明:直線![]() 過(guò)定點(diǎn).
過(guò)定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某企業(yè)有![]() ,
,![]() 兩個(gè)分廠生產(chǎn)某種產(chǎn)品,規(guī)定該產(chǎn)品的某項(xiàng)質(zhì)量指標(biāo)值不低于130的為優(yōu)質(zhì)品.分別從
兩個(gè)分廠生產(chǎn)某種產(chǎn)品,規(guī)定該產(chǎn)品的某項(xiàng)質(zhì)量指標(biāo)值不低于130的為優(yōu)質(zhì)品.分別從![]() ,
,![]() 兩廠中各隨機(jī)抽取100件產(chǎn)品統(tǒng)計(jì)其質(zhì)量指標(biāo)值,得到如圖頻率分布直方圖:
兩廠中各隨機(jī)抽取100件產(chǎn)品統(tǒng)計(jì)其質(zhì)量指標(biāo)值,得到如圖頻率分布直方圖:
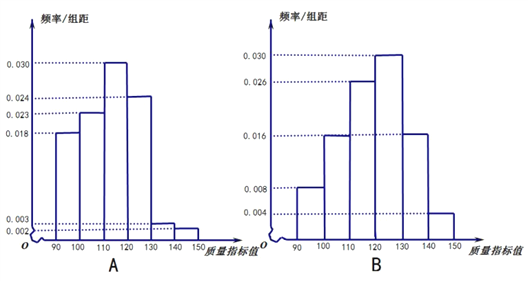
(1)根據(jù)頻率分布直方圖,分別求出![]() 分廠的質(zhì)量指標(biāo)值的眾數(shù)和中位數(shù)的估計(jì)值;
分廠的質(zhì)量指標(biāo)值的眾數(shù)和中位數(shù)的估計(jì)值;
(2)填寫![]() 列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有
列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有![]() 的把握認(rèn)為這兩個(gè)分廠的產(chǎn)品質(zhì)量有差異?
的把握認(rèn)為這兩個(gè)分廠的產(chǎn)品質(zhì)量有差異?
優(yōu)質(zhì)品 | 非優(yōu)質(zhì)品 | 合計(jì) | |
| |||
| |||
合計(jì) |
(3)(i)從![]() 分廠所抽取的100件產(chǎn)品中,利用分層抽樣的方法抽取10件產(chǎn)品,再?gòu)倪@10件產(chǎn)品中隨機(jī)抽取2件,已知抽到一件產(chǎn)品是優(yōu)質(zhì)品的條件下,求抽取的兩件產(chǎn)品都是優(yōu)質(zhì)品的概率;
分廠所抽取的100件產(chǎn)品中,利用分層抽樣的方法抽取10件產(chǎn)品,再?gòu)倪@10件產(chǎn)品中隨機(jī)抽取2件,已知抽到一件產(chǎn)品是優(yōu)質(zhì)品的條件下,求抽取的兩件產(chǎn)品都是優(yōu)質(zhì)品的概率;
(ii)將頻率視為概率,從![]() 分廠中隨機(jī)抽取10件該產(chǎn)品,記抽到優(yōu)質(zhì)品的件數(shù)為
分廠中隨機(jī)抽取10件該產(chǎn)品,記抽到優(yōu)質(zhì)品的件數(shù)為![]() ,求
,求![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 上是奇函數(shù).
上是奇函數(shù).
(1)求![]() ;
;
(2)對(duì)![]() ,不等式
,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)令![]() ,若關(guān)于
,若關(guān)于![]() 的方程
的方程![]() 有唯一實(shí)數(shù)解,求實(shí)數(shù)
有唯一實(shí)數(shù)解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】研究變量![]() ,
,![]() 得到一組樣本數(shù)據(jù),進(jìn)行回歸分析,有以下結(jié)論
得到一組樣本數(shù)據(jù),進(jìn)行回歸分析,有以下結(jié)論
①殘差平方和越小的模型,擬合的效果越好;
②用相關(guān)指數(shù)![]() 來(lái)刻畫回歸效果,
來(lái)刻畫回歸效果,![]() 越小說(shuō)明擬合效果越好;
越小說(shuō)明擬合效果越好;
③在回歸直線方程![]() 中,當(dāng)解釋變量
中,當(dāng)解釋變量![]() 每增加1個(gè)單位時(shí),預(yù)報(bào)變量
每增加1個(gè)單位時(shí),預(yù)報(bào)變量![]() 平均增加0.2個(gè)單位
平均增加0.2個(gè)單位
④若變量![]() 和
和![]() 之間的相關(guān)系數(shù)為
之間的相關(guān)系數(shù)為![]() ,則變量
,則變量![]() 和
和![]() 之間的負(fù)相關(guān)很強(qiáng),以上正確說(shuō)法的個(gè)數(shù)是( )
之間的負(fù)相關(guān)很強(qiáng),以上正確說(shuō)法的個(gè)數(shù)是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】生物學(xué)家預(yù)言,21世紀(jì)將是細(xì)菌發(fā)電造福人類的時(shí)代。說(shuō)起細(xì)菌發(fā)電,可以追溯到1910年,英國(guó)植物學(xué)家利用鉑作為電極放進(jìn)大腸桿菌的培養(yǎng)液里,成功地制造出世界上第一個(gè)細(xì)菌電池。然而各種細(xì)菌都需在最適生長(zhǎng)溫度的范圍內(nèi)生長(zhǎng)。當(dāng)外界溫度明顯高于最適生長(zhǎng)溫度,細(xì)菌被殺死;如果在低于細(xì)菌的最低生長(zhǎng)溫度時(shí),細(xì)菌代謝活動(dòng)受抑制。為了研究某種細(xì)菌繁殖的個(gè)數(shù)![]() 是否與在一定范圍內(nèi)的溫度
是否與在一定范圍內(nèi)的溫度![]() 有關(guān),現(xiàn)收集了該種細(xì)菌的6組觀測(cè)數(shù)據(jù)如下表:
有關(guān),現(xiàn)收集了該種細(xì)菌的6組觀測(cè)數(shù)據(jù)如下表:

經(jīng)計(jì)算得:![]() ,
,![]() ,線性回歸模型的殘差平方和
,線性回歸模型的殘差平方和![]() .其中
.其中![]() 分別為觀測(cè)數(shù)據(jù)中的溫度與繁殖數(shù),
分別為觀測(cè)數(shù)據(jù)中的溫度與繁殖數(shù),![]() .
.
參考數(shù)據(jù):![]() ,
,![]() ,
,
(Ⅰ)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() (精確到0.1);
(精確到0.1);
(Ⅱ)若用非線性回歸模型求得![]() 關(guān)于
關(guān)于![]() 回歸方程為
回歸方程為![]() ,且非線性回歸模型的殘差平方和
,且非線性回歸模型的殘差平方和![]() .
.
(ⅰ)用相關(guān)指數(shù)![]() 說(shuō)明哪種模型的擬合效果更好;
說(shuō)明哪種模型的擬合效果更好;
(ⅱ)用擬合效果好的模型預(yù)測(cè)溫度為34℃時(shí)該種細(xì)菌的繁殖數(shù)(結(jié)果取整數(shù)).
附:一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計(jì)為
的斜率和截距的最小二乘法估計(jì)為 ,
,![]() ;
;
相關(guān)指數(shù)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com