分析:(Ⅰ)設出等比數列的公比,利用對于任意的n∈N
+有S
n,S
n+2,S
n+1成等差得2S
3=S
1+S
2,代入首項和公比后即可求得公比,再由已知
a1+a4=-,代入公比后可求得首項,則數列{a
n}的通項公式可求;
(Ⅱ)把(Ⅰ)中求得的a
n和已知b
n=n代入
||整理,然后利用錯位相減法求T
n,把T
n代入(n-1)
2≤m(T
n-n-1)后分離變量m,使問題轉化為求函數的最大值問題,分析函數的單調性時可用作差法.
解答:解:(Ⅰ)設等比數列{a
n}的公比為q,
∵對于任意的n∈N
+有S
n,S
n+2,S
n+1成等差,
∴2
(a1+a1q+a1q2)=a1+a1+a1q.
整理得:
2a1(1+q+q2)=a1(2+q).
∵a
1≠0,∴,2+2q+2q
2=2+q.
∴2q
2+q=0,又q≠0,∴q=
-.
又
a1+a4=a1(1+q3)=-,
把q=
-代入后可得
a1=-.
所以,
an=a1qn-1=(-)×(-)n-1=(-)n;
(Ⅱ)∵b
n=n,
an=(-)n,∴
||=||=n•2n,
∴
Tn=1×21+2×22+3×23+…+n•2n.
2Tn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1.
∴
-Tn=2+22+23+…+2n-n•2n+1=
-n•2n+1∴
Tn=-(-n•2n+1)=(n-1)•2n+1+2.
若(n-1)
2≤m(T
n-n-1)對于n≥2恒成立,
則(n-1)
2≤m[(n-1)•2
n+1+2-n-1]對于n≥2恒成立,
也就是(n-1)
2≤m(n-1)•(2
n+1-1)對于n≥2恒成立,
∴m≥
對于n≥2恒成立,
令
f(n)=,
∵
f(n+1)-f(n)=-=
| (2-n)•2n+1-1 |
| (2n+2-1)(2n+1-1) |
<0∴f(n)為減函數,∴f(n)≤f(2)=
=.
∴m
≥.
所以,(n-1)
2≤m(T
n-n-1)對于n≥2恒成立的實數m的范圍是[
,+∞).
點評:本題考查了等比數列的通項公式,考查了錯位相減法求數列的前n項和,考查了數列的函數特性,訓練了利用分離變量法求參數的取值范圍,解答此題的關鍵在于判斷分離變量后的函數的單調性,利用了比較大小的基本方法-作差法.
此題屬中高檔題.




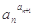 為定值,則稱數列{an}為“等冪數列”.已知數列{an}為“等冪數列”,且a1=2,a2=4,Sn為數列{an}的前n項和,則S2009= ( )A.6026
B .6024 C.2
D.4
為定值,則稱數列{an}為“等冪數列”.已知數列{an}為“等冪數列”,且a1=2,a2=4,Sn為數列{an}的前n項和,則S2009= ( )A.6026
B .6024 C.2
D.4