
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),在以
為參數(shù)),在以![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標(biāo)系中,射線
軸的正半軸為極軸的極坐標(biāo)系中,射線![]() ,與
,與![]() ,
,![]() 各有一個交點,當(dāng)
各有一個交點,當(dāng)![]() 時,這兩個交點間的距離為2,當(dāng)
時,這兩個交點間的距離為2,當(dāng)![]() ,這兩個交點重合.
,這兩個交點重合.
(1)分別說明![]() ,
,![]() 是什么曲線,并求出
是什么曲線,并求出![]() 與
與![]() 的值;
的值;
(2)設(shè)當(dāng)![]() 時,
時,![]() 與
與![]() ,
,![]() 的交點分別為
的交點分別為![]() ,當(dāng)
,當(dāng)![]() ,
,![]() 與
與![]() ,
,![]() 的交點分別為
的交點分別為![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
【答案】(1)詳見解析;(2)![]()
【解析】
試題分析:(1)有曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]()
(![]() 為參數(shù)),消去參數(shù)的
為參數(shù)),消去參數(shù)的![]() 是圓,
是圓,![]() 是橢圓,并利用.當(dāng)
是橢圓,并利用.當(dāng)![]() 時,這兩個交點間的距離為
時,這兩個交點間的距離為![]() ,當(dāng)
,當(dāng)![]() 時,這兩個交點重合,求出
時,這兩個交點重合,求出![]() 及
及![]() .(2)利用
.(2)利用![]() 的普通方程,當(dāng)
的普通方程,當(dāng)![]() 時,
時,![]() 與
與![]() 的交點分別為
的交點分別為![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() 與
與![]() 的交點為
的交點為![]() ,利用面積公式求出面積.
,利用面積公式求出面積.
試題解析:(1)![]() 是圓,
是圓,![]() 是橢圓.
是橢圓.
當(dāng)![]() 時,射線
時,射線![]() 與
與![]() ,
,![]() 交點的直角坐標(biāo)分別是
交點的直角坐標(biāo)分別是![]() 因為這兩點間的距離為2,所以
因為這兩點間的距離為2,所以![]()
當(dāng)![]() ,射線
,射線![]() 與
與![]() ,
,![]() 交點的直角坐標(biāo)分別是
交點的直角坐標(biāo)分別是![]() 因為這兩點重合,所以
因為這兩點重合,所以![]() ;
;
(2)![]() ,
,![]() 的普通方程為
的普通方程為![]()
當(dāng)![]() 時,射線
時,射線![]() 與
與![]() 交點
交點![]() 的橫縱表是
的橫縱表是![]() ,與
,與![]() 交點
交點![]() 的橫坐標(biāo)是
的橫坐標(biāo)是![]()
當(dāng)![]() 時,射線
時,射線![]() 與
與![]() ,
,![]() 的兩個交點
的兩個交點![]() 分別與交點
分別與交點![]() 關(guān)于
關(guān)于![]() 軸對稱,因此四邊形
軸對稱,因此四邊形![]() 為梯形,故四邊形
為梯形,故四邊形![]() 的面積為
的面積為![]() .
.


 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的三個內(nèi)角A、B、C所對的邊分別是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范圍.
,求a+c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面為矩形,D為
的底面為矩形,D為![]() 的中點,AC⊥平面BCC1B1.
的中點,AC⊥平面BCC1B1.
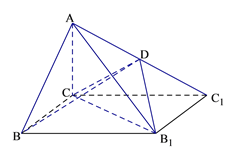
(Ⅰ)證明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的長;
(2)求B1D與平面ABB1所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=![]() ,AD=CD=1.
,AD=CD=1.
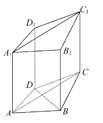
(1)求證:BD⊥AA1.
(2)在棱BC上取一點E,使得AE∥平面DCC1D1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】f(x)是定義在R上的奇函數(shù),對x,y∈R都有f(x+y)=f(x)+f(y),且當(dāng)x>0時,f(x)<0,f(-1)=2.
(1)求證:f(x)為奇函數(shù);
(2)求證:f(x)是R上的減函數(shù);
(3)求f(x)在[-2,4]上的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】共享單車是城市慢行系統(tǒng)的一種模式創(chuàng)新,對于解決民眾出行“最后一公里”的問題特別見效,由于停取方便、租用價格低廉,各色共享單車受到人們的熱捧.某自行車廠為共享單車公司生產(chǎn)新樣式的單車,已知生產(chǎn)新樣式單車的固定成本為20000元,每生產(chǎn)一件新樣式單車需要增加投入100元.根據(jù)初步測算,自行車廠的總收益(單位:元)滿足分段函數(shù)![]() ,其中
,其中
![]() 是新樣式單車的月產(chǎn)量(單位:件),利潤
是新樣式單車的月產(chǎn)量(單位:件),利潤![]() 總收益
總收益![]() 總成本.
總成本.
(1)試將自行車廠的利潤![]() 元表示為月產(chǎn)量
元表示為月產(chǎn)量![]() 的函數(shù);
的函數(shù);
(2)當(dāng)月產(chǎn)量為多少件時自行車廠的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知如圖,六棱錐P-ABCDEF的底面是正六邊形,PA⊥平面ABCDEF.則下列結(jié)論不正確的是( )
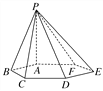
A. CD∥平面PAF
B. DF⊥平面PAF
C. CF∥平面PAB
D. CF⊥平面PAD
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某同學(xué)用“五點法”畫函數(shù)f(x)=Asin(ωx+φ)在某一個周期內(nèi)的圖象時,列表并填入的數(shù)據(jù)如下表:
x |
| x1 |
| x2 | x3 |
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(1)求x1,x2,x3的值及函數(shù)f(x)的表達式;
(2)將函數(shù)f(x)的圖象向左平移π個單位,可得到函數(shù)g(x)的圖象,求函數(shù)y=f(x)·g(x)在區(qū)間![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 時,
時, ![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com