
【題目】已知數列{an}中,a1=1,a2=a,且an+1=k(an+an+2)對任意正整數n都成立,數列{an}的前n項和為Sn.
(1)若![]() ,且S2019=2019,求a;
,且S2019=2019,求a;
(2)是否存在實數k,使數列{an}是公比不為1的等比數列,且任意相鄰三項am,am+1,am+2按某順序排列后成等差數列,若存在,求出所有k的值;若不存在,請說明理由;
(3)若![]() ,求Sn.
,求Sn.
【答案】(1) a=1;(2)存在滿足要求的實數k有且僅有一個![]()
![]() ;(3) Sn=
;(3) Sn=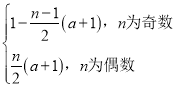
【解析】
(1)由題意求得首項為1,公差d=a-1,結合等差數列前n項和公式列方程可得a;
(2)假設存在滿足題意的實數k,分類討論可得k;
(3)k=![]()
![]() ,an+1=
,an+1=![]()
![]() (an+an+2),an+2+an+1=
(an+an+2),an+2+an+1=![]() (an+1+an),an+3+an+2=
(an+1+an),an+3+an+2=![]() (an+2+an+1)=an+1+an,結合題意分類討論,然后分組求和可得Sn.
(an+2+an+1)=an+1+an,結合題意分類討論,然后分組求和可得Sn.
解:(1)k=![]() ,an+1=
,an+1=![]() (an+an+2),
(an+an+2),
∴數列{an}為等差數列,
∵a1=1,a2=a,∴公差d=a-1,
∴S2019=2019=2019+![]() ×(a-1),解得a=1;
×(a-1),解得a=1;
(2)設數列{an}是公比不為1的等比數列,則它的公比q=![]() =a,
=a,
∴am=am-1,am+1=am,am+2=am+1,任意相鄰三項
am,am+1,am+2按某順序排列后成等差數列,
①an+1為等差中項,則2am+1=am+am+2.
即am-1+am+1=2am,解得a=1,不合題意;
②am為等差中項,則2am=am+1+am+2,
即2am-1=am+1+am,化簡a2+a-2=0,解得a=-2或a=1(舍去);
③若am+2為等差中項,則2am+2=am+1+am,
即2am+1=am+am-1,化簡得:2a2-a-1=0,解得a=![]()
![]() ;
;
∴k=![]() =
=![]() =
=![]() =
=![]()
![]() .
.
綜上可得,滿足要求的實數k有且僅有一個![]()
![]() ;
;
(3)k=![]()
![]() ,則an+1=
,則an+1=![]()
![]() (an+an+2),
(an+an+2),
∴an+2+an+1=![]() (an+1+an),an+3+an+2=
(an+1+an),an+3+an+2=![]() (an+2+an+1)=an+1+an,
(an+2+an+1)=an+1+an,
當n是偶數時,Sn=a1+a2+…+an=(a1+a2)+…+(an-1+an)
=![]() (a1+a2)=
(a1+a2)=![]() (a+1).
(a+1).
當n是奇數時,Sn=a1+(a2+a3)+…+(an-1+an)
=1+![]() (a2+a3)=1+
(a2+a3)=1+![]() [-(a1+a2)]=1
[-(a1+a2)]=1![]()
![]() (a+1)(n≥1),
(a+1)(n≥1),
n=1也適合上式,
綜上可得,Sn=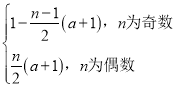 .
.


科目:高中數學 來源: 題型:
【題目】楊輝三角,是二項式系數在三角形中的一種幾何排列.在歐洲,這個表叫做帕斯卡三角形,帕斯卡(1623-1662)是在1654年發現這一規律的.我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表,這是我國數學史上的一個偉大成就.如圖所示,在“楊輝三角”中,去除所有為1的項,依次構成數列![]() ,則此數列前135項的和為( )
,則此數列前135項的和為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,過點
,過點![]() 向圓
向圓![]() 引兩條切線
引兩條切線![]() ,
,![]() ,切點為
,切點為![]() ,
,![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,則直線
,則直線![]() 的方程為____________;若
的方程為____________;若![]() 為直線
為直線![]() 上一動點,則直線
上一動點,則直線![]() 經過定點__________.
經過定點__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著電子閱讀的普及,傳統紙質媒體遭受到了強烈的沖擊.某雜志社近9年來的紙質廣告收入如下表所示:

根據這9年的數據,對![]() 和
和![]() 作線性相關性檢驗,求得樣本相關系數的絕對值為0.243;
作線性相關性檢驗,求得樣本相關系數的絕對值為0.243;
根據后5年的數據,對![]() 和
和![]() 作線性相關性檢驗,求得樣本相關系數的絕對值為0.984.
作線性相關性檢驗,求得樣本相關系數的絕對值為0.984.
(1)如果要用線性回歸方程預測該雜志社2019年的紙質廣告收入,現在有兩個方案,
方案一:選取這9年數據進行預測,方案二:選取后5年數據進行預測.
從實際生活背景以及線性相關性檢驗的角度分析,你覺得哪個方案更合適?
附:相關性檢驗的臨界值表:
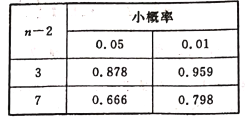
(2)某購物網站同時銷售某本暢銷書籍的紙質版本和電子書,據統計,在該網站購買該書籍的大量讀者中,只購買電子書的讀者比例為![]() ,紙質版本和電子書同時購買的讀者比例為
,紙質版本和電子書同時購買的讀者比例為![]() ,現用此統計結果作為概率,若從上述讀者中隨機調查了3位,求購買電子書人數多于只購買紙質版本人數的概率.
,現用此統計結果作為概率,若從上述讀者中隨機調查了3位,求購買電子書人數多于只購買紙質版本人數的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面命題正確的是( )
A.“![]() ”是“
”是“![]() ”的 充 分不 必 要條件
”的 充 分不 必 要條件
B.命題“若![]() ,則
,則![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,則
,則![]() ”.
”.
C.設![]() ,則“
,則“![]() 且
且![]() ”是“
”是“![]() ”的必要而不充分條件
”的必要而不充分條件
D.設![]() ,則“
,則“![]() ”是“
”是“![]() ”的必要 不 充 分 條件
”的必要 不 充 分 條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 軸交于
軸交于![]() 點,與
點,與![]() 軸交于
軸交于![]() 點,記
點,記![]() 與坐標軸圍成的三角形
與坐標軸圍成的三角形![]() 的面積為
的面積為![]() .
.
(1)若![]() ,且
,且![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)若![]() 、
、![]() 都在正半軸上,求
都在正半軸上,求![]() 的最小值;
的最小值;
(3)寫出面積![]() 的取值范圍與直線
的取值范圍與直線![]() 條數的對應關系.(不需要證明)
條數的對應關系.(不需要證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的長軸長為4,焦距為
的長軸長為4,焦距為![]()
(Ⅰ)求橢圓![]() 的方程;
的方程;
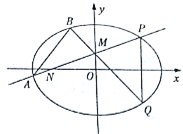
(Ⅱ)過動點![]() 的直線交
的直線交![]() 軸與點
軸與點![]() ,交
,交![]() 于點
于點![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是線段
是線段![]() 的中點.過點
的中點.過點![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于另一點
于另一點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() .
.
(ⅰ)設直線![]() 的斜率分別為
的斜率分別為![]() ,證明
,證明![]() 為定值;
為定值;
(ⅱ)求直線![]() 的斜率的最小值.
的斜率的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com