
【題目】已知函數(shù)![]()
(1)求函數(shù)在區(qū)間![]() 上的最小值;
上的最小值;
(2)討論![]() 在區(qū)間
在區(qū)間![]() 上的極值.
上的極值.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,無極值;當
時,無極值;當![]()
【解析】
(1)對函數(shù)![]() 進行求導,然后利用導函數(shù)判斷
進行求導,然后利用導函數(shù)判斷![]() 上單調性,求出極值,最后求出最小值;
上單調性,求出極值,最后求出最小值;
(2)利用導數(shù)求出函數(shù)的單調區(qū)間,根據(jù)區(qū)間的端點值對![]() 的取值,進行分類,在每種情況下,判斷函數(shù)是否具有極值,沒有,說明理由,有求出.
的取值,進行分類,在每種情況下,判斷函數(shù)是否具有極值,沒有,說明理由,有求出.
(1)![]() ,
,
當![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 單調遞增,因此
單調遞增,因此![]() 是極小值點,極小值為
是極小值點,極小值為![]() ,所以函數(shù)
,所以函數(shù)![]() 上的最小值為
上的最小值為![]() ;
;
(2)![]() ,
,
所以當![]() 時,
時,![]() ,函數(shù)函數(shù)
,函數(shù)函數(shù)![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調遞減,當
單調遞減,當![]() 時,
時,![]() ,函數(shù)函數(shù)
,函數(shù)函數(shù)![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調遞減,所以函數(shù)
單調遞減,所以函數(shù)![]() 沒有極值;
沒有極值;
當![]() 時,當
時,當![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 單調遞增,因此
單調遞增,因此![]() 是極小值點,極小值為
是極小值點,極小值為![]() .
.


 亮點激活精編提優(yōu)100分大試卷系列答案
亮點激活精編提優(yōu)100分大試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和
項和![]() 滿足:
滿足:![]() ,數(shù)列
,數(shù)列![]() 滿足:對任意
滿足:對任意![]() 有
有![]()
![]() .
.
(1)求數(shù)列![]() 與數(shù)列
與數(shù)列![]() 的通項公式;
的通項公式;
(2)記![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,證明:當
,證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】按照《國務院關于印發(fā)“十三五”節(jié)能減排綜合工作方案的通知》(國發(fā)〔2016〕74號)的要求,到2020年,全國二氧化硫排放總量要控制在1580萬噸以內,要比2015年下降15%.假設“十三五”期間每一年二氧化硫排放總量下降的百分比都相等,2015年后第![]() 年的二氧化硫律放總量最大值為
年的二氧化硫律放總量最大值為![]() 萬噸.
萬噸.
(1)求![]() 的解析式;
的解析式;
(2)求2019年全國二氧化賴持放總量要控制在多少萬晚以內(精確到1萬噸).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數(shù)方程為
,其參數(shù)方程為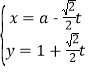 (
(![]() 為參數(shù),
為參數(shù),![]() ),以坐標原點為極點,以
),以坐標原點為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點(
兩點(![]() 在
在![]() 之間),且
之間),且![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)常年生產(chǎn)一種出口產(chǎn)品,根據(jù)預測可知,進入![]() 世紀以來,該產(chǎn)品的產(chǎn)量平穩(wěn)增長.記
世紀以來,該產(chǎn)品的產(chǎn)量平穩(wěn)增長.記![]() 年為第
年為第![]() 年,且前
年,且前![]() 年中,第
年中,第![]() 年與年產(chǎn)量
年與年產(chǎn)量![]() 萬件之間的關系如下表所示:
萬件之間的關系如下表所示:
|
|
|
|
|
|
|
|
|
|
若![]() 近似符合以下三種函數(shù)模型之一:
近似符合以下三種函數(shù)模型之一:![]() ,
,![]() ,
,![]() .
.
(1)找出你認為最適合的函數(shù)模型,并說明理由,然后選取其中你認為最適合的數(shù)據(jù)求出相應的解析式;
(2)因遭受某國對該產(chǎn)品進行反傾銷的影響,![]() 年的年產(chǎn)量比預計減少
年的年產(chǎn)量比預計減少![]() ,試根據(jù)所建立的函數(shù)模型,確定
,試根據(jù)所建立的函數(shù)模型,確定![]() 年的年產(chǎn)量.
年的年產(chǎn)量.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】從分別寫有1,2,3,4,5的5張卡片中隨機抽取1張,放回后再隨機抽取1張,則抽得的第一張卡片上的數(shù)大于第二張卡片上的數(shù)的概率為()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】因客流量臨時增大,某鞋店擬用一個高為50![]() (即
(即![]() )的平面鏡自制一個豎直擺放的簡易鞋鏡,根據(jù)經(jīng)驗:一般顧客
)的平面鏡自制一個豎直擺放的簡易鞋鏡,根據(jù)經(jīng)驗:一般顧客![]() 的眼睛
的眼睛![]() 到地面的距離為
到地面的距離為![]() (
(![]() )在區(qū)間
)在區(qū)間![]() 內,設支架
內,設支架![]() 高為
高為![]() (
(![]() )
)![]() ,
,![]() ,顧客可視的鏡像范圍為
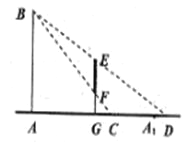
,顧客可視的鏡像范圍為![]() (如圖所示),記
(如圖所示),記![]() 的長度為
的長度為![]() (
(![]() ).
).
(I)當![]() 時,試求
時,試求![]() 關于
關于![]() 的函數(shù)關系式和
的函數(shù)關系式和![]() 的最大值;
的最大值;
(II)當顧客的鞋![]() 在鏡中的像
在鏡中的像![]() 滿足不等關系
滿足不等關系![]() (不計鞋長)時,稱顧客可在鏡中看到自己的鞋,若使一般顧客都能在鏡中看到自己的鞋,試求
(不計鞋長)時,稱顧客可在鏡中看到自己的鞋,若使一般顧客都能在鏡中看到自己的鞋,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了解高校學生平均每天使用手機的時間長短是否與性別有關,某調查小組隨機抽取了25 名男生、10名女生進行為期一周的跟蹤調查,調查結果如表所示:
平均每天使用手機 | 平均每天使用手機 | 合計 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合計 | 18 | 17 | 35 |
(I)在參與調查的平均每天使用手機不超過3小時的7名女生中,有4人使用國產(chǎn)手機,從這7名女生中任意選取2人,求至少有1人使用國產(chǎn)手機的概率;
(II) 根據(jù)列聯(lián)表,是否有90%的把握認為學生使用手機的時間長短與性別有關(![]() 的觀測值
的觀測值![]() 精確到0.01).
精確到0.01).
附:
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
參考公式: 
![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com