
���}Ŀ����֪���ֱ��![]() ��
��![]() ��ԓ�������ϵă��c(di��n)��
��ԓ�������ϵă��c(di��n)��![]() ��
��![]() ���t���F
���t���F![]() ���w�e��_______.
���w�e��_______.
���𰸡�![]()
��������
�O(sh��)���Ğ��c(di��n)O����AB���c(di��n)D���B��OD��CD���f��SC�����ֱ�����������Ҷ����������ε���e��ʽ���S��SCD�������F�ĸ�AB������������F���w�e��
���O(sh��)���Ğ��c(di��n)O����AB���c(di��n)D���B��OD��CD����?y��n)龀��SC�����ֱ����
������Ҳ�Ǵ�A��ֱ�����t�ã���SAC=��SBC=90��
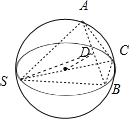
������Rt��SAC�У�SC=4����ASC=30�� �ã�AC=2��SA=2![]()
����Rt��SBC�У�SC=4����BSC=30�� �ã�BC=2��SB=2![]() �t��SA=SB��AC=BC
�t��SA=SB��AC=BC
��?y��n)��c(di��n)D��AB�����c(di��n)�����ڵ���������ASB�У�SD��AB��SD=![]() =
=![]() =
=![]()
�ڵ���������CAB�У�CD��AB��CD=![]() =
=![]() =
=![]()
��SD��CD���c(di��n)D ���ԣ�AB��ƽ��SCD �������FS��ABC���w�e��V=![]() ABS��SCD��
ABS��SCD��
��?y��n)飺SD=![]() ��CD=
��CD=![]() ��SC=4 ���������Ҷ����ã�cos��SDC=��SD2+CD2��SC2��
��SC=4 ���������Ҷ����ã�cos��SDC=��SD2+CD2��SC2��![]() =��
=��![]() +
+![]() ��16��
��16��![]() =
=![]() =
=![]()
�t��sin��SDC=![]() =
=![]()
����������e��ʽ����SCD����eS=![]() SDCDsin��SDC=
SDCDsin��SDC=![]() =3
=3
���ԣ����FS��ABC���w�e��V=![]() ABS��SCD=
ABS��SCD=![]() =
=![]()
�ʴ𰸞���![]() ��
��



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������՚��|(zh��)���������F�����F(xi��n)����F(xi��n)���࣬�����ȾΣ������.�����Ⱦ�������ļ¡��������y���ķμ���.���˽�ij���ķμ����Ƿ��c�Ԅe���P(gu��n)����ij�t(y��)Ժ�S�C(j��)���ķμ�����Ժ��![]() ���M(j��n)�І����{(di��o)�飬�õ������µ���(li��n)����
���M(j��n)�І����{(di��o)�飬�õ������µ���(li��n)����
���ķμ��� | �����ķμ��� | ��Ӌ(j��) | |
�� |
|
|
|
Ů |
|
|
|
��Ӌ(j��) |
|
|
|
��1���÷ӳ�ӵķ����ڻ��ķμ�������Ⱥ�г�![]() �ˣ��������Գ�����ˣ�
�ˣ��������Գ�����ˣ�
��2����������ȡ��![]() �����x
�����x![]() �ˣ���ǡ����
�ˣ���ǡ����![]() ��Ů�Եĸ��ʣ�
��Ů�Եĸ��ʣ�
��3�������о��ķμ����Ƿ��c�Ԅe���P(gu��n)��ՈӋ(j��)����y(t��ng)Ӌ(j��)��![]() �����ж������J(r��n)���ķμ����c�Ԅe���P(gu��n)��
�����ж������J(r��n)���ķμ����c�Ԅe���P(gu��n)��
������R��ֵ����������
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
������ʽ��  ������
������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��У�@��(zh��n)��G��һ�Kֱ����![]() �İ�A�οյأ��c(di��n)
�İ�A�οյأ��c(di��n)![]() �ڰ�A�A���ϣ���
�ڰ�A�A���ϣ���![]() ��ĵط��N�ݣ���
��ĵط��N�ݣ���![]() �ă�(n��i)��������
�ă�(n��i)��������![]() ��һˮ�أ�
��һˮ�أ�![]() ��
��![]() ��
��![]() ߅�ϣ�������ط��N������
߅�ϣ�������ط��N������![]() ��
�� ![]() ���O(sh��)��
���O(sh��)��![]() ����e��
����e��![]() ����������e��
����������e��![]() ��
��
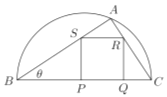
��1����![]() ��
��![]() ��ʾ
��ʾ![]() ��
��![]() ��
��
��2����(d��ng)![]() �̶���
�̶���![]() ׃���r����
׃���r����![]() ��Сֵ���˕r�Ľ�
��Сֵ���˕r�Ľ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�̈�����ӆُһ�N�����ů�⣬ÿ�N��һ�_�@����200Ԫ��δ�N�۵Įa(ch��n)Ʒ���؏S�ң�ÿ�_̝�p50Ԫ������(j��)����Ľ�(j��ng)�(y��n)��ÿ����������c��(d��ng)�����͚�����P(gu��n)�������͚��λ�څ^(q��)�g![]() ����������100�_����͚��λ�څ^(q��)�g
����������100�_����͚��λ�څ^(q��)�g![]() ����������200�_����͚��λ�څ^(q��)�g
����������200�_����͚��λ�څ^(q��)�g![]() ����������300�_����˾�N�۲����˴_��11�·ݵ�ӆُӋ(j��)�����y(t��ng)Ӌ(j��)��ǰ����11�·ݸ������͚��?c��i)?sh��)��(j��)���õ�������l��(sh��)�ֲ�����
����������300�_����˾�N�۲����˴_��11�·ݵ�ӆُӋ(j��)�����y(t��ng)Ӌ(j��)��ǰ����11�·ݸ������͚��?c��i)?sh��)��(j��)���õ�������l��(sh��)�ֲ�����
��͚��(��) |
|
|
|
|
|
�씵(sh��) | 11 | 25 | 36 | 16 | 2 |
����͚��λ�ڸ��^(q��)�g���l�ʴ�����͚��λ��ԓ�^(q��)�g�ĸ���.
��11�·��@�N�ů��ÿ��������![]() (��λ���_)�ķֲ��У�
(��λ���_)�ķֲ��У�
����˾�N�۲���ÿ���N������![]() (��λ��Ԫ)�Ĕ�(sh��)�W(xu��)������Q������(j��)��Ӌ(j��)��11�·�ÿ��ӆُ200�_��250�_������֮���x��һ����(y��ng)�x�Ă���
(��λ��Ԫ)�Ĕ�(sh��)�W(xu��)������Q������(j��)��Ӌ(j��)��11�·�ÿ��ӆُ200�_��250�_������֮���x��һ����(y��ng)�x�Ă���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
����ӑՓ![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
������![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ����Ȼ����(sh��)�ĵה�(sh��)����
����Ȼ����(sh��)�ĵה�(sh��)����
��������(d��ng)![]() �r��������
�r��������![]() ���c(di��n)
���c(di��n)![]() ̎���о��c����(bi��o)�S���ɵ������ε���e��
̎���о��c����(bi��o)�S���ɵ������ε���e��
��������![]() �څ^(q��)�g
�څ^(q��)�g![]() �Ϻ��������(sh��)��(sh��)
�Ϻ��������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�����L(f��ng)���^(q��)�l(f��)�еļo(j��)���¼���Ͷ���Ј�������(j��)�Ј��{(di��o)����r���A(y��)Ӌ(j��)ÿöԓ�o(j��)���µ��Ј��ry����λ��Ԫ���c���Еr�gx����λ���죩�Ĕ�(sh��)��(j��)���£�
���Еr�gx�� | 2 | 6 | 20 |
�Ј��ryԪ | 102 | 78 | 120 |
��1������(j��)�ϱ픵(sh��)��(j��)�������к���(sh��)���xȡһ��ǡ��(d��ng)?sh��)ĺ��?sh��)����ԓ�o(j��)���µ��Ј��ry�c���Еr�gx��׃���P(gu��n)ϵ���f�����ɣ���![]() ����
����![]() ����
����![]() ��
��
��2���������xȡ�ĺ���(sh��)����ԓ�o(j��)�����Ј��r��͕r�������씵(sh��)����͵ăr��
��3���������xȡ�ĺ���(sh��)��������![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ��������(sh��)��(sh��)k��ȡֵ����.
��������(sh��)��(sh��)k��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ��
��![]() �錍(sh��)��(sh��)���Ľ⼯��
�錍(sh��)��(sh��)���Ľ⼯��![]() ������
������![]() .
.
��1����![]() ����
����![]() ��ȡֵ������
��ȡֵ������
��2����![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
(1)��(sh��)![]() ����Сֵ��
����Сֵ��![]() ȡ����Сֵ�r��׃��x�ļ��ϣ�
ȡ����Сֵ�r��׃��x�ļ��ϣ�
(2)ָ������(sh��)y��![]() �ĈD������ɺ���(sh��)y��sinx�ĈD��(j��ng)�^��Щ׃�Q�õ���
�ĈD������ɺ���(sh��)y��sinx�ĈD��(j��ng)�^��Щ׃�Q�õ���
(3)��(d��ng)x��[0��m]�r������(sh��)y��f(x)��ֵ��?y��n)?/span>![]() ����(sh��)��(sh��)m��ȡֵ������
����(sh��)��(sh��)m��ȡֵ������
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com