
���}Ŀ����D����������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n)���c(di��n)
�����c(di��n)���c(di��n)![]() ��ƽ��
��ƽ��![]() ��(n��i)����Ӱ�ھ�(xi��n)��
��(n��i)����Ӱ�ھ�(xi��n)��![]() ��.
��.
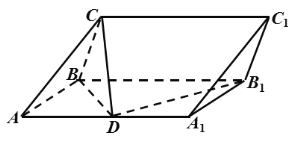
(1)���C��![]() ��
��
(2)��![]() ������������������
������������������![]() ���w�e.
���w�e.
���𰸡���1��Ҋ(ji��n)�C����(2) ![]()
��������
��1���քe�C��![]() ��
��![]() ���Y(ji��)��ֱ��(xi��n)�cƽ�洹ֱ�ж������ɡ���2����һ��Ӌ(j��)��
���Y(ji��)��ֱ��(xi��n)�cƽ�洹ֱ�ж������ɡ���2����һ��Ӌ(j��)��![]() ���Y(ji��)��
���Y(ji��)��![]() ��
��![]() �����ɡ����� :Ӌ(j��)��
�����ɡ����� :Ӌ(j��)��![]() ���Y(ji��)��
���Y(ji��)��![]() ��Ӌ(j��)���w�e�����ɡ��������Y(ji��)��
��Ӌ(j��)���w�e�����ɡ��������Y(ji��)��![]() ��Ӌ(j��)��Y(ji��)�������ɡ�
��Ӌ(j��)��Y(ji��)�������ɡ�
(1)�C�����O(sh��)�c(di��n)![]() ��ƽ��
��ƽ��![]() ��(n��i)����Ӱ��
��(n��i)����Ӱ��![]() ��
��

�t![]() ��
��![]() ����
����![]() ����
����![]() ������
������![]() .
.
��![]() ��
��![]() ��
��![]() ��
��
�t![]() ����
����![]() ��
��![]() ��
��![]() ��
��
�t![]() ��
��
��![]() ����
����![]() .
.
��![]() ����
����![]() .
.
(2)��һ��![]() ��
��
��(1)��![]() ����
����![]() �������F
�������F![]() �ĸߣ�
�ĸߣ�
![]() ����������
����������![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
�����������w�e![]() ����������
����������![]() ���w�e��
���w�e��![]() .
.
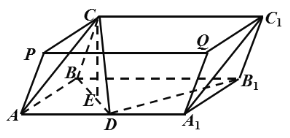
���������������a(b��)����������D����![]() �Ҹ�һ�ӣ�
�Ҹ�һ�ӣ�
��![]() ��
��
��![]() ��
��
��(1)��![]() ����
����![]() ��������
��������![]() �ĸߣ�
�ĸߣ�
�� ��
��
��![]() ����������
����������![]() ���w�e��
���w�e��![]() .
.
�������������F![]() ����(1)��
����(1)��![]() ��
��![]() �������F
�������F![]() �ĸߣ�6��
�ĸߣ�6��
ӛ![]() ��ƽ��
��ƽ��![]() �ľ��x��
�ľ��x��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��
![]() ��
��![]() �����c(di��n)����
�����c(di��n)����![]() ��ƽ��
��ƽ��![]() �ľ��x��
�ľ��x��![]() ��
��
![]() .
.
��������![]() ���w�e��
���w�e��![]() .
.


 �����������㑪(y��ng)���}ϵ�д�
�����������㑪(y��ng)���}ϵ�д� ͬ����չ��xϵ�д�
ͬ����չ��xϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2����![]() ���C����
���C����![]() ��
��
��3����![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() �����C����
�����C����![]() .
.
��������(sh��)��(j��)��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
(��)��(d��ng)![]() �r(sh��)��������(xi��n)
�r(sh��)��������(xi��n)![]() ���c(di��n)
���c(di��n)![]() ̎���о�(xi��n)���̣�
̎���о�(xi��n)���̣�
(��)��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ���Сֵ��-2������
�ϵ���Сֵ��-2������![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��)����(sh��)��(sh��)
����Ȼ��(du��)��(sh��)�ĵה�(sh��)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��
������![]() ��
��![]() ��(n��i)���{(di��o)�f�p����(sh��)��(sh��)
��(n��i)���{(di��o)�f�p����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
����������(sh��)![]() �Ѓɂ�(g��)�Oֵ�c(di��n)�քe��
�Ѓɂ�(g��)�Oֵ�c(di��n)�քe��![]() ��
��![]() ���C����
���C����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����(du��)��![]() ��(g��)
��(g��)![]() ��
��![]() ��(g��)
��(g��)![]() ��
��![]() ��(g��)
��(g��)![]() �ųɵ��У������������¶��xһ�У�������һ����һ��(g��)��ĸ��.�����^�ϵăɂ�(g��)��ĸ��ͬ���t��ԓλ�Ì�(xi��)�ϵ�����(g��)��ĸ�������^�ϵăɂ�(g��)��ĸ��ͬ���t��ԓλ�Ì�(xi��)��ԓ��ĸ.��(du��)�µõ������؏�(f��)����IJ�����ֱ��׃?y��u)�һ��(g��)��ĸ��ֹ.�D�o����
�ųɵ��У������������¶��xһ�У�������һ����һ��(g��)��ĸ��.�����^�ϵăɂ�(g��)��ĸ��ͬ���t��ԓλ�Ì�(xi��)�ϵ�����(g��)��ĸ�������^�ϵăɂ�(g��)��ĸ��ͬ���t��ԓλ�Ì�(xi��)��ԓ��ĸ.��(du��)�µõ������؏�(f��)����IJ�����ֱ��׃?y��u)�һ��(g��)��ĸ��ֹ.�D�o����![]() ��һ��(g��)����.
��һ��(g��)����.

�����е�������(sh��)![]() ��ʹ�Ì�(du��)����ij�ʼ���У���(j��ng)�������������õ��������ε�����(g��)��c(di��n)�ϵ���ĸҪôȫ��ͬ��Ҫô�Ƀɲ�ͬ.
��ʹ�Ì�(du��)����ij�ʼ���У���(j��ng)�������������õ��������ε�����(g��)��c(di��n)�ϵ���ĸҪôȫ��ͬ��Ҫô�Ƀɲ�ͬ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��
(1)��![]() ��
��![]() �ĘOֵ����
�ĘOֵ����![]() ��ֵ������
��ֵ������![]() �Ć��{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
(2)��![]() �r(sh��)��
�r(sh��)��![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ֱ������(bi��o)ϵ��![]() �У�����(xi��n)
�У�����(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() �酢��(sh��)��
�酢��(sh��)�� ![]() ��. ������(bi��o)ԭ�c(di��n)��O�c(di��n)��
��. ������(bi��o)ԭ�c(di��n)��O�c(di��n)�� ![]() �S�����S��O�S�����O����(bi��o)ϵ����ֱ֪��(xi��n)
�S�����S��O�S�����O����(bi��o)ϵ����ֱ֪��(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1���O(sh��)![]() ������(xi��n)
������(xi��n)![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)����(d��ng)
�ϵ�һ��(g��)��(d��ng)�c(di��n)����(d��ng)![]() �r(sh��)�����c(di��n)
�r(sh��)�����c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x�����ֵ��
�ľ��x�����ֵ��
��2��������(xi��n)![]() �����е��c(di��n)����ֱ��(xi��n)
�����е��c(di��n)����ֱ��(xi��n)![]() �����·�����
�����·�����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������w![]() �У�
��![]() ��
�� ![]() ��
��

��1���C����![]() ��
��
��2����![]() ��
��![]() �������w
�������w![]() ���w�e��2��������
���w�e��2��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��(xi��n)
�У�ֱ��(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�����S��O�S�������O����(bi��o)ϵ����֪����(xi��n)
�S�����S��O�S�������O����(bi��o)ϵ����֪����(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1����ֱ��(xi��n)![]() ����ͨ�����c����(xi��n)
����ͨ�����c����(xi��n)![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���O(sh��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com