
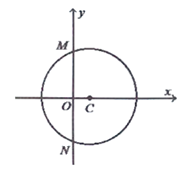
【題目】已知圓心在x軸正半軸上的圓C與直線![]() 相切,與y軸交于M,N兩點,且
相切,與y軸交于M,N兩點,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求圓C的標準方程;
求圓C的標準方程;
![]() Ⅱ
Ⅱ![]() 過點
過點![]() 的直線l與圓C交于不同的兩點D,E,若
的直線l與圓C交于不同的兩點D,E,若![]() 時,求直線l的方程;
時,求直線l的方程;
![]() Ⅲ
Ⅲ![]() 已知Q是圓C上任意一點,問:在x軸上是否存在兩定點A,B,使得
已知Q是圓C上任意一點,問:在x軸上是否存在兩定點A,B,使得![]() ?若存在,求出A,B兩點的坐標;若不存在,請說明理由.
?若存在,求出A,B兩點的坐標;若不存在,請說明理由.
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() ;(III)存在
;(III)存在![]() ,
,![]() 或
或![]() ,
,![]() 滿足題意.
滿足題意.
【解析】
![]() 設圓C的方程為
設圓C的方程為![]() ,利用點C到直線
,利用點C到直線![]() 的距離為
的距離為![]() ,求出a,即可求圓C的標準方程;
,求出a,即可求圓C的標準方程;
![]() Ⅱ
Ⅱ![]() 設直線l的方程為
設直線l的方程為![]() 即
即![]() ,則由題意可知,圓心C到直線l的距離
,則由題意可知,圓心C到直線l的距離![]() ,即可求出k的值,
,即可求出k的值,
![]() Ⅲ
Ⅲ![]() 方法一:假設在x軸上存在兩定點
方法一:假設在x軸上存在兩定點![]() ,
,![]() ,設
,設![]() 是圓C上任意一點,由題意可得則
是圓C上任意一點,由題意可得則![]() ,即可求出a,b的值,
,即可求出a,b的值,
方法二:設![]() 是圓C上任意一點,由
是圓C上任意一點,由![]() 得
得![]() ,對照圓C的標準方程
,對照圓C的標準方程![]() 即
即![]() ,可得
,可得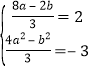 ,解得即可.
,解得即可.
解:![]() Ⅰ
Ⅰ![]() 由題意知圓心
由題意知圓心![]() ,且
,且![]() ,
,
由![]() 知
知![]() 中,
中,![]() ,
,![]() ,則
,則![]() ,
,
于是可設圓C的方程為![]()
又點C到直線![]() 的距離為
的距離為![]() ,
,
所以![]() 或
或![]() 舍
舍![]() ,
,
故圓C的方程為![]() ,
,
![]() Ⅱ
Ⅱ![]() 設直線l的方程為
設直線l的方程為![]() 即
即![]() ,則由題意可知,圓心C到直線l的距離
,則由題意可知,圓心C到直線l的距離![]() ,
,
故![]() ,解得
,解得![]() ,
,
又當![]() 時滿足題意,
時滿足題意,
因此所求的直線方程為![]() 或
或![]() ,
,
![]() Ⅲ
Ⅲ![]() 方法一:假設在x軸上存在兩定點
方法一:假設在x軸上存在兩定點![]() ,
,![]() ,設
,設![]() 是圓C上任意一點,則
是圓C上任意一點,則![]() 即
即![]() ,
,
則![]() ,
,
令![]() ,
,
解得![]() 或
或![]() ,
,
因此存在![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() 滿足題意,
滿足題意,
方法二:設![]() 是圓C上任意一點,
是圓C上任意一點,
由![]() 得
得![]() ,
,
化簡可得![]() ,
,
對照圓C的標準方程![]() 即
即![]() ,
,
可得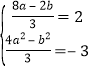 ,
,
解得解得![]() 或
或![]() ,
,
因此存在![]() ,
,![]() 或
或![]() ,
,![]() 滿足題意.
滿足題意.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】給定函數![]() ,若對于定義域中的任意
,若對于定義域中的任意![]() ,都有
,都有![]()
![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為“爬坡函數”.
為“爬坡函數”.
(Ⅰ)證明:函數![]() 是“爬坡函數”;
是“爬坡函數”;
(Ⅱ)若函數![]() 是“爬坡函數”,求實數
是“爬坡函數”,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若對任意的實數![]() ,函數
,函數![]() 都不是“爬坡函數”,求實數
都不是“爬坡函數”,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)滿足xf′(x)﹣f(x)>0,當0<m<n<1時,下面選項中最大的一項是( )
A.![]()
B.logmn?f(lognm)
C.![]()
D.lognm?f(logmn)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃投資A、B兩種金融產品,根據市場調查與預測,A產品的利潤與投資量成正比例,其關系如圖1,B產品的利潤與投資量的算術平方根成正比例,其關系如圖2(注:利潤與投資量的單位:萬元).
(1)分別將A、B兩產品的利潤表示為投資量的函數關系式;
(2)該公司已有10萬元資金,并全部投入A、B兩種產品中,問:怎樣分配這10萬元投資,才能使公司獲得最大利潤?其最大利潤為多少萬元?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了對教師教學水平和教師管理水平進行評價,從該校學生中選出300人進行統計.其中對教師教學水平給出好評的學生人數為總數的60%,對教師管理水平給出好評的學生人數為總數的75%,其中對教師教學水平和教師管理水平都給出好評的有120人.
(1)填寫教師教學水平和教師管理水平評價的2×2列聯表:
對教師管理水平好評 | 對教師管理水平不滿意 | 合計 | |
對教師教學水平好評 | |||
對教師教學水平不滿意 | |||
合計 |
問:是否可以在犯錯誤概率不超過0.1%的前提下,認為教師教學水平好評與教師管理水平好評有關、
(2)若將頻率視為概率,有4人參與了此次評價,設對教師教學水平和教師管理水平全好評的人數為隨機變量X;
①求對教師教學水平和教師管理水平全好評的人數X的分布列(概率用組合數算式表示);
②求X的數學期望和方差.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中數學 來源: 題型:
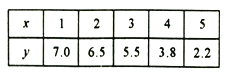
【題目】為了了解某地區某種農產品的年產量![]() (單位:噸)對價格
(單位:噸)對價格![]() (單位:千元/噸)和利潤
(單位:千元/噸)和利潤![]() 的影響,對近五年該農產品的年產量和價格統計如下表:
的影響,對近五年該農產品的年產量和價格統計如下表:
參考公式: 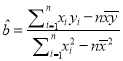 ,
, ![]() .
.
根據參考公式,以求得![]()
(1)求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若每噸該農產品的成本為2千元,假設該農產品可全部賣出,預測當年產量為多少時,年利潤![]() 取到最大值?(保留兩位小數)
取到最大值?(保留兩位小數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com