
已知函數(shù)f(x)=alnx+x2 (a為實常數(shù)).
(1)當a=﹣4時,求函數(shù)f(x)的單調(diào)區(qū)間;
(2)當x∈[1,e]時,討論方程f(x)=0根的個數(shù);
(3)若 a>0,且對任意的x1,x2∈[1,e],都有|f(x1)﹣f(x2)![]() ,求實數(shù)a的取值范圍.
,求實數(shù)a的取值范圍.
考點:
利用導數(shù)研究函數(shù)的單調(diào)性;根的存在性及根的個數(shù)判斷;導數(shù)在最大值、最小值問題中的應用.
專題:
導數(shù)的綜合應用.
分析:
(1)當a=﹣4時,利用導數(shù)的運算法則可得![]() ,在區(qū)間(0,+∞)上分別解出f′(x)>0和f′(x)<0即可得出單調(diào)區(qū)間;
,在區(qū)間(0,+∞)上分別解出f′(x)>0和f′(x)<0即可得出單調(diào)區(qū)間;
(2)當x=1時,方程f(x)=0無解.
當x≠1時,方程f(x)=0(x∈[1,e])等價于方程 ![]() (x∈(1,e]).
(x∈(1,e]).
設g(x)=![]() ,則
,則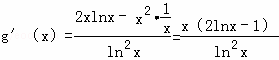 .分別解出g′(x)>0與g′(x)<0即可得出單調(diào)性,
.分別解出g′(x)>0與g′(x)<0即可得出單調(diào)性,
又g(e)=e2,![]() ,作出y=g(x)與直線y=﹣a的圖象,由圖象可知a的范圍與方程根的關系;
,作出y=g(x)與直線y=﹣a的圖象,由圖象可知a的范圍與方程根的關系;
(3)若a>0時,f(x)在區(qū)間[1,e]上是增函數(shù),函數(shù)![]() 在區(qū)間[1,e]上是減函數(shù).
在區(qū)間[1,e]上是減函數(shù).
不妨設1≤x1≤x2≤e,則![]() 等價于
等價于![]() .
.
即![]() ,即函數(shù)
,即函數(shù)![]() 在x∈[1,e]時是減函數(shù).
在x∈[1,e]時是減函數(shù).
可得![]() ,即
,即![]() 在x∈[1,e]時恒成立.再利用
在x∈[1,e]時恒成立.再利用![]() 在x∈[1,e]時是減函數(shù),即可得出實數(shù)a的取值范圍.
在x∈[1,e]時是減函數(shù),即可得出實數(shù)a的取值范圍.
解答:
解:(1)當a=﹣4時,![]() ,
,
當![]() 時,f'(x)<0;當
時,f'(x)<0;當![]() 時,f'(x)>0.
時,f'(x)>0.
∴f(x)的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() .
.
(2)當x=1時,方程f(x)=0無解.
當x≠1時,方程f(x)=0(x∈[1,e])等價于方程 ![]() (x∈(1,e]).
(x∈(1,e]).
設g(x)=![]() ,則
,則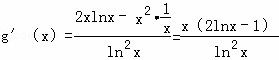 .
.
當![]() 時,g'(x)<0,函數(shù)g(x)遞減,
時,g'(x)<0,函數(shù)g(x)遞減,
當![]() 時,g'(x)>0,函數(shù)g(x)遞增.
時,g'(x)>0,函數(shù)g(x)遞增.
又g(e)=e2,![]() ,作出y=g(x)與直線y=﹣a的圖象,由圖象知:
,作出y=g(x)與直線y=﹣a的圖象,由圖象知:
當2e<﹣a≤e2時,即﹣e2≤a<﹣2e時,方程f(x)=0有2個相異的根;
當a<﹣e2或a=﹣2e時,方程f(x)=0有1個根;
當a>﹣2e時,方程f(x)=0有0個根.
(3)若a>0時,f(x)在區(qū)間[1,e]上是增函數(shù),函數(shù)![]() 在區(qū)間[1,e]上是減函數(shù).
在區(qū)間[1,e]上是減函數(shù).
不妨設1≤x1≤x2≤e,
則![]() 等價于
等價于![]() .
.
即![]() ,
,
即函數(shù)![]() 在x∈[1,e]時是減函數(shù).
在x∈[1,e]時是減函數(shù).
∴![]() ,即
,即![]() 在x∈[1,e]時恒成立.
在x∈[1,e]時恒成立.
∵![]() 在x∈[1,e]時是減函數(shù),∴
在x∈[1,e]時是減函數(shù),∴![]() .
.
所以,實數(shù)a的取值范圍是![]() .
.
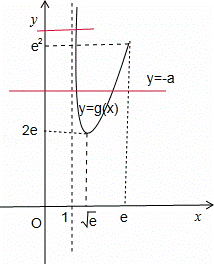
點評:
本題綜合考查了利用導數(shù)研究函數(shù)的單調(diào)性、等價轉化、適當變形等基礎知識與基本技能,考查了數(shù)形結合思想方法、推理能力和計算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 3 | 4 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
|
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com