
【題目】如圖甲,已知矩形![]() 中,
中, ![]() 為
為![]() 上一點,且
上一點,且![]() ,垂足為
,垂足為![]() ,現將矩形
,現將矩形![]() 沿對角線
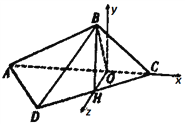
沿對角線![]() 折起,得到如圖乙所示的三棱錐
折起,得到如圖乙所示的三棱錐![]() .
.

(Ⅰ)在圖乙中,若![]() ,求
,求![]() 的長度;
的長度;
(Ⅱ)當二面角![]() 等于
等于![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() (2)余弦值為
(2)余弦值為![]() .
.
【解析】試題分析:(Ⅰ)當![]() 時,由線面垂直的判定定理,可得
時,由線面垂直的判定定理,可得![]() 平面
平面![]() ,所以
,所以![]() ,由勾股定理求出BH的長度;(Ⅱ)以
,由勾股定理求出BH的長度;(Ⅱ)以![]() 為坐標原點,
為坐標原點, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,垂直于平面
軸,垂直于平面![]() 的方向為
的方向為![]() 軸建系,可得平面ADC的法向量為
軸建系,可得平面ADC的法向量為![]() ,由當二面角
,由當二面角![]() 等于
等于![]() ,求出點B,C,H三點的坐標,假設平面
,求出點B,C,H三點的坐標,假設平面![]() 的法向量
的法向量![]() ,由
,由![]() ,求出
,求出![]() ,根據兩向量的夾角公式,求出二面角
,根據兩向量的夾角公式,求出二面角![]() 的余弦值.
的余弦值.
試題解析:(Ⅰ)由![]() ,可得折疊后
,可得折疊后![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
解得![]() ,
, ![]() ,由勾股定理,
,由勾股定理,
![]() .
.
(Ⅱ)如圖,以![]() 為坐標原點,
為坐標原點, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,垂直于平面
軸,垂直于平面![]() 的方向為
的方向為![]() 軸建系,
軸建系,
可得平面![]() 的法向量為
的法向量為![]() ,
,
即有![]() ,再由二面角
,再由二面角![]() 等于
等于![]() ,
,
可得![]() 點坐標為
點坐標為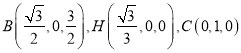 ,
,
所以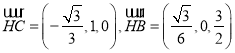 ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則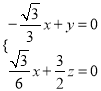
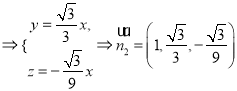 ,
,
所以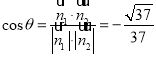 ,
,
由橫坐標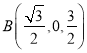 大于
大于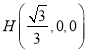 橫坐標,
橫坐標,
所以二面角![]() 為鈍角,所以余弦值為
為鈍角,所以余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2﹣4x+3,若f(x)≥mx對任意的實數x≥2都成立,則實數m的取值范圍是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=x2+2(a﹣1)x+2在區間[﹣1,2]上單調,則實數a的取值范圍為( )
A.[2,+∞)
B.(﹣∞,﹣1]
C.(﹣∞,﹣1]∪[2,+∞)
D.(﹣∞,﹣1)∪(2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校![]() 屆高三文(1)班在一次數學測驗中,全班
屆高三文(1)班在一次數學測驗中,全班![]() 名學生的數學成績的頻率分布直方圖如下,已知分數在
名學生的數學成績的頻率分布直方圖如下,已知分數在![]() 的學生數有
的學生數有![]() 人.
人.
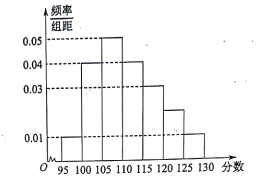
(1)求總人數![]() 和分數在
和分數在![]() 的人數
的人數![]() ;
;
(2)利用頻率分布直方圖,估算該班學生數學成績的眾數和中位數各是多少?
(3)現在從比分數在![]() 名學生(男女生比例為
名學生(男女生比例為![]() )中任選
)中任選![]() 人,求其中至多含有
人,求其中至多含有![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com