
下列說法中,正確的有 .
①若點 是拋物線
是拋物線 上一點,則該點到拋物線的焦點的距離是
上一點,則該點到拋物線的焦點的距離是 ;
;
②設(shè) 、
、 為雙曲線
為雙曲線 的兩個焦點,
的兩個焦點, 為雙曲線上一動點,
為雙曲線上一動點, ,則
,則 的面積為
的面積為 ;
;
③設(shè)定圓 上有一動點
上有一動點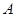 ,圓
,圓 內(nèi)一定點
內(nèi)一定點 ,
, 的垂直平分線與半徑
的垂直平分線與半徑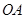 的交點為點
的交點為點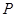 ,則
,則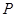 的軌跡為一橢圓;
的軌跡為一橢圓;
④設(shè)拋物線焦點到準線的距離為 ,過拋物線焦點
,過拋物線焦點 的直線交拋物線于A、B兩點,則
的直線交拋物線于A、B兩點,則 、
、 、
、 成等差數(shù)列.
成等差數(shù)列.
①④
【解析】
試題分析:根據(jù)題意,由于①若點 是拋物線
是拋物線 上一點,則該點到拋物線的焦點的距離是
上一點,則該點到拋物線的焦點的距離是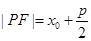 ;根據(jù)定義顯然得到成立。
;根據(jù)定義顯然得到成立。
②設(shè) 、
、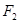 為雙曲線
為雙曲線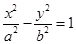 的兩個焦點,
的兩個焦點, 為雙曲線上一動點
為雙曲線上一動點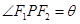 ,則
,則 的面積為
的面積為 ;結(jié)合定義和余弦定理可知面積為
;結(jié)合定義和余弦定理可知面積為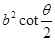 ,故錯誤。
,故錯誤。
③設(shè)定圓 上有一動點
上有一動點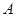 ,圓
,圓 內(nèi)一定點
內(nèi)一定點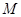 ,
,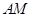 的垂直平分線與半徑
的垂直平分線與半徑 的交點為點
的交點為點 ,則
,則 的軌跡為一橢圓;不一定。錯誤
的軌跡為一橢圓;不一定。錯誤
④設(shè)拋物線焦點到準線的距離為 ,過拋物線焦點
,過拋物線焦點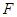 的直線交拋物線于A、B兩點,則
的直線交拋物線于A、B兩點,則 、
、 、
、 成等差數(shù)列.聯(lián)立方程組,結(jié)合韋達定理可以證明得到
成等差數(shù)列.聯(lián)立方程組,結(jié)合韋達定理可以證明得到 +
+ =
= ,進而說明結(jié)論成立,故答案為①④
,進而說明結(jié)論成立,故答案為①④
考點:圓錐曲線的性質(zhì)
點評:主要是考查了圓錐曲線的方程以及性質(zhì)的運用,屬于中檔題。


科目:高中數(shù)學 來源: 題型:
| π |
| 3 |
| π |
| 6 |
| ∫ | 1 -1 |
| 1-x2 |
| π |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 1 |
| 10 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| p |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| θ |
| 2 |
| 1 |
| |AF| |
| 1 |
| p |
| 1 |
| |BF| |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com