
ĪŠŅ}─┐Ī┐╦─éĆ(g©©)═¼śė┤¾ąĪĄ─Ū“![]() ,
,![]() ,
,![]() ,
,![]() ā╔ā╔ŽÓŪą,³c(di©Żn)
ā╔ā╔ŽÓŪą,³c(di©Żn)![]() ╩ŪŪ“
╩ŪŪ“![]() ╔ŽĄ─äė(d©░ng)³c(di©Żn),ätų▒ŠĆ
╔ŽĄ─äė(d©░ng)³c(di©Żn),ätų▒ŠĆ![]() ┼cų▒ŠĆ
┼cų▒ŠĆ![]() ╦∙│╔ĮŪĄ─ėÓŽęųĄĄ─╚ĪųĄĘČć·×ķŻ© Ż®
╦∙│╔ĮŪĄ─ėÓŽęųĄĄ─╚ĪųĄĘČć·×ķŻ© Ż®
A. B.
B. C.
C.![]() D.
D.
ĪŠ┤░ĖĪ┐C
ĪŠĮŌ╬÷Ī┐
ę“?y©żn)ķ╦─éĆ(g©©)═¼śė┤¾ąĪĄ─Ū“![]() ,
,![]() ,
,![]() ,
,![]() ā╔ā╔ŽÓŪą,┐╔Ą├
ā╔ā╔ŽÓŪą,┐╔Ą├![]() ╩Ūš²╦─├µ¾w,įO(sh©©)▀ģķL×ķ
╩Ūš²╦─├µ¾w,įO(sh©©)▀ģķL×ķ![]() ,▀^
,▀^![]() ū„
ū„![]() Ąū├µ
Ąū├µ![]() ,▀\(y©┤n)ė├ŠĆ├µ┤╣ų▒Ą─ąį┘|(zh©¼),╝┤┐╔Ą├ĄĮ╦∙│╔ĮŪĄ─ūŅ┤¾ųĄ,į┘ė╔┤¾łAĄ─ŪąŠĆėŗ(j©¼)╦Ń┐╔Ą├╦∙│╔ĮŪĄ─ūŅąĪųĄ,╝┤┐╔Ū¾Ą├ų▒ŠĆ
,▀\(y©┤n)ė├ŠĆ├µ┤╣ų▒Ą─ąį┘|(zh©¼),╝┤┐╔Ą├ĄĮ╦∙│╔ĮŪĄ─ūŅ┤¾ųĄ,į┘ė╔┤¾łAĄ─ŪąŠĆėŗ(j©¼)╦Ń┐╔Ą├╦∙│╔ĮŪĄ─ūŅąĪųĄ,╝┤┐╔Ū¾Ą├ų▒ŠĆ![]() ┼cų▒ŠĆ
┼cų▒ŠĆ![]() ╦∙│╔ĮŪĄ─ėÓŽęųĄĄ─╚ĪųĄĘČć·.
╦∙│╔ĮŪĄ─ėÓŽęųĄĄ─╚ĪųĄĘČć·.
╚ńłD
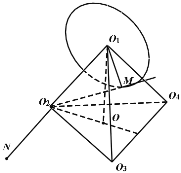
![]() ╩Ūš²╦─├µ¾w,įO(sh©©)▀ģķL×ķ
╩Ūš²╦─├µ¾w,įO(sh©©)▀ģķL×ķ![]() ,
,
▀^![]() ū„
ū„![]() Ąū├µ
Ąū├µ![]() ┐╔Ą├
┐╔Ą├![]() ×ķĄū├µĄ─ųąą─,
×ķĄū├µĄ─ųąą─,
ė╔![]() ,┐╔Ą├
,┐╔Ą├![]() ,ät
,ät![]() į┌ų▒ŠĆ
į┌ų▒ŠĆ![]() ╔ŽĢr(sh©¬),
╔ŽĢr(sh©¬),
┐╔Ą├ų▒ŠĆ![]() ┼cų▒ŠĆ
┼cų▒ŠĆ![]() ┤╣ų▒,╝┤ėą╦∙│╔ĮŪĄ─ėÓŽęųĄ×ķ
┤╣ų▒,╝┤ėą╦∙│╔ĮŪĄ─ėÓŽęųĄ×ķ![]() ,
,
ū„![]() ,ät
,ät![]() ,į┌ŲĮ├µ
,į┌ŲĮ├µ![]() ā╚(n©©i),▀^
ā╚(n©©i),▀^![]() ū„Ū“Ą─ŪąŠĆŻ¼
ū„Ū“Ą─ŪąŠĆŻ¼
įO(sh©©)Ūą³c(di©Żn)×ķ![]() ,┤╦Ģr(sh©¬)
,┤╦Ģr(sh©¬)![]() ūŅ┤¾,┐╔Ą├
ūŅ┤¾,┐╔Ą├![]()
![]() ┼c
┼c![]() │╔Ą─ūŅ┤¾ĮŪ
│╔Ą─ūŅ┤¾ĮŪ![]()
![]() Ż¼
Ż¼
![]()
![]() Ą─ūŅąĪųĄ×ķ
Ą─ūŅąĪųĄ×ķ![]() Ż¼
Ż¼
![]()
![]() ┼c
┼c![]() │╔Ą─ūŅąĪĮŪ×ķ
│╔Ą─ūŅąĪĮŪ×ķ![]() ,╝┤ėą╦∙│╔ĮŪĄ─ėÓŽęųĄ×ķ
,╝┤ėą╦∙│╔ĮŪĄ─ėÓŽęųĄ×ķ![]() Ż¼
Ż¼
![]() ų▒ŠĆ
ų▒ŠĆ![]() ┼cų▒ŠĆ
┼cų▒ŠĆ![]() ╦∙│╔ĮŪĄ─ėÓŽęųĄĄ─╚ĪųĄĘČć·×ķ
╦∙│╔ĮŪĄ─ėÓŽęųĄĄ─╚ĪųĄĘČć·×ķ![]() .
.
╣╩▀x:C.


 ▌pŪ╔ŖZ╣┌ų▄£yį┬┐╝ų▒═©ųą┐╝ŽĄ┴ą┤░Ė
▌pŪ╔ŖZ╣┌ų▄£yį┬┐╝ų▒═©ųą┐╝ŽĄ┴ą┤░Ė
| ─Ļ╝ē(j©¬) | Ė▀ųąšn│╠ | ─Ļ╝ē(j©¬) | │§ųąšn│╠ |
| Ė▀ę╗ | Ė▀ę╗├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ | │§ę╗ | │§ę╗├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ |
| Ė▀Č■ | Ė▀Č■├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ | │§Č■ | │§Č■├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ |
| Ė▀╚² | Ė▀╚²├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ | │§╚² | │§╚²├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ |
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐─│▐r(n©«ng)┐Ų╦∙ī”(du©¼)Č¼╝ŠĢāę╣£ž▓Ņ┤¾ąĪ┼c─│Ę┤╝Š╣Ø(ji©”)┤¾Č╣ą┬ŲĘĘN░l(f©Ī)č┐ČÓ╔┘ų«ķg▀M(j©¼n)ąąĘų╬÷蹊┐Ż¼╦¹éāĘųäeėøõø┴╦12į┬1╚šų┴12į┬5╚šĄ─├┐╠ņĢāę╣£ž▓Ņ┼cīŹ(sh©¬)“×(y©żn)╩ę├┐╠ņ├┐100┐├ĘNūėųąĄ─░l(f©Ī)č┐öĄ(sh©┤)Ż¼Ą├ĄĮ╚ńŽ┬┘Y┴ŽŻ║
╚šŲ┌ | 12į┬1╚š | 12į┬2╚š | 12į┬3╚š | 12į┬4╚š | 12į┬5╚š |
£ž▓Ņ | 10 | 11 | 13 | 12 | 8 |
░l(f©Ī)č┐ | 23 | 25 | 30 | 26 | 16 |
įō▐r(n©«ng)┐Ų╦∙┤_Č©Ą─蹊┐ĘĮ░Ė╩ŪŻ║Ž╚Å─▀@5ĮMöĄ(sh©┤)ō■(j©┤)ųą▀x╚Ī3ĮMöĄ(sh©┤)ō■(j©┤)Ū¾ŠĆąį╗žÜwĘĮ│╠Ż¼į┘ė├╩ŻŽ┬Ą─2ĮMöĄ(sh©┤)ō■(j©┤)▀M(j©¼n)ąąÖz“×(y©żn)Ż«
(1)╚¶▀x╚ĪĄ─3ĮMöĄ(sh©┤)ō■(j©┤)ŪĪ║├╩Ū▀B└m(x©┤)![]() ╠ņĄ─öĄ(sh©┤)ō■(j©┤)(
╠ņĄ─öĄ(sh©┤)ō■(j©┤)(![]() ▒Ē╩ŠöĄ(sh©┤)ō■(j©┤)üĒūį╗ź▓╗ŽÓÓÅĄ─╚²╠ņ)Ż¼Ū¾
▒Ē╩ŠöĄ(sh©┤)ō■(j©┤)üĒūį╗ź▓╗ŽÓÓÅĄ─╚²╠ņ)Ż¼Ū¾![]() Ą─Ęų▓╝┴ą╝░Ų┌═¹Ż║
Ą─Ęų▓╝┴ą╝░Ų┌═¹Ż║
(2)Ė∙ō■(j©┤)12į┬2╚šų┴4╚šöĄ(sh©┤)ō■(j©┤)Ż¼Ū¾│÷░l(f©Ī)č┐öĄ(sh©┤)![]() ĻP(gu©Īn)ė┌£ž▓Ņ
ĻP(gu©Īn)ė┌£ž▓Ņ![]() Ą─ŠĆąį╗žÜwĘĮ│╠
Ą─ŠĆąį╗žÜwĘĮ│╠![]() Ż«ė╔╦∙Ū¾Ą├ŠĆąį╗žÜwĘĮĄŠĄ├ĄĮĄ─╣└ėŗ(j©¼)öĄ(sh©┤)ō■(j©┤)┼c╩ŻŽ┬Ą─Öz“×(y©żn)öĄ(sh©┤)ō■(j©┤)Ą─š`▓ŅŠ∙▓╗│¼▀^2ŅwŻ¼ätšJ(r©©n)×ķĄ├ĄĮĄ─ŠĆąį╗žÜwĘĮ│╠╩Ū┐╔┐┐Ą─Ż¼įćå¢╦∙Ą├Ą─ŠĆąį╗žÜwĘĮ│╠╩Ūʱ┐╔┐┐Ż┐
Ż«ė╔╦∙Ū¾Ą├ŠĆąį╗žÜwĘĮĄŠĄ├ĄĮĄ─╣└ėŗ(j©¼)öĄ(sh©┤)ō■(j©┤)┼c╩ŻŽ┬Ą─Öz“×(y©żn)öĄ(sh©┤)ō■(j©┤)Ą─š`▓ŅŠ∙▓╗│¼▀^2ŅwŻ¼ätšJ(r©©n)×ķĄ├ĄĮĄ─ŠĆąį╗žÜwĘĮ│╠╩Ū┐╔┐┐Ą─Ż¼įćå¢╦∙Ą├Ą─ŠĆąį╗žÜwĘĮ│╠╩Ūʱ┐╔┐┐Ż┐
ĖĮŻ║ģó┐╝╣½╩ĮŻ║ Ż«
Ż«
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐─│▐r(n©«ng)┐Ų╦∙ī”(du©¼)Č¼╝ŠĢāę╣£ž▓Ņ┤¾ąĪ┼c─│Ę┤╝Š╣Ø(ji©”)┤¾Č╣ą┬ŲĘĘN░l(f©Ī)č┐ČÓ╔┘ų«ķgĄ─ĻP(gu©Īn)ŽĄ▀M(j©¼n)ąąĘų╬÷蹊┐Ż¼╦¹éāĘųäeėøõø┴╦12į┬1╚šų┴12į┬5╚šĄ─├┐╠ņĢāę╣£ž▓Ņ┼cīŹ(sh©¬)“×(y©żn)╩ę├┐╠ņ├┐100ŅwĘNūėųąĄ─░l(f©Ī)č┐öĄ(sh©┤)Ż¼Ą├ĄĮ╚ńŽ┬┘Y┴ŽŻ║
╚šŲ┌ | 12į┬2╚š | 12į┬3╚š | 12į┬4╚š |
£ž▓Ņ | 11 | 13 | 12 |
░l(f©Ī)č┐öĄ(sh©┤) | 25 | 30 | 26 |
Ż©1Ż®šłĖ∙ō■(j©┤)12į┬2╚šų┴12į┬4╚šĄ─öĄ(sh©┤)ō■(j©┤)Ż¼Ū¾│÷![]() ĻP(gu©Īn)ė┌
ĻP(gu©Īn)ė┌![]() Ą─ŠĆąį╗žÜwĘĮ│╠
Ą─ŠĆąį╗žÜwĘĮ│╠![]() Ż╗
Ż╗
Ż©2Ż®įō▐r(n©«ng)┐Ų╦∙┤_Č©Ą─蹊┐ĘĮ░Ė╩ŪŻ║Ž╚ė├╔Ž├µĄ─3ĮMöĄ(sh©┤)ō■(j©┤)Ū¾ŠĆąį╗žÜwĘĮ│╠Ż¼į┘▀x╚Ī2ĮMöĄ(sh©┤)ō■(j©┤)▀M(j©¼n)ąąÖz“×(y©żn)Ż«╚¶12į┬5╚š£ž▓Ņ×ķ![]() Ż¼░l(f©Ī)č┐öĄ(sh©┤)16ŅwŻ¼12į┬6╚š£ž▓Ņ×ķ
Ż¼░l(f©Ī)č┐öĄ(sh©┤)16ŅwŻ¼12į┬6╚š£ž▓Ņ×ķ![]() Ż¼░l(f©Ī)č┐öĄ(sh©┤)23ŅwŻ«ė╔ŠĆąį╗žÜwĘĮ│╠Ą├ĄĮĄ─╣└ėŗ(j©¼)öĄ(sh©┤)ō■(j©┤)┼c╦∙▀x│÷Ą─Öz“×(y©żn)öĄ(sh©┤)ō■(j©┤)Ą─š`▓ŅŠ∙▓╗│¼▀^2ŅwŻ¼ätšJ(r©©n)×ķĄ├ĄĮĄ─ŠĆąį╗žÜwĘĮ│╠╩Ū┐╔┐┐Ą─Ż¼įćå¢Ż©1Ż®ųą╦∙Ą├Ą─ŠĆąį╗žÜwĘĮ│╠╩Ūʱ┐╔┐┐Ż┐
Ż¼░l(f©Ī)č┐öĄ(sh©┤)23ŅwŻ«ė╔ŠĆąį╗žÜwĘĮ│╠Ą├ĄĮĄ─╣└ėŗ(j©¼)öĄ(sh©┤)ō■(j©┤)┼c╦∙▀x│÷Ą─Öz“×(y©żn)öĄ(sh©┤)ō■(j©┤)Ą─š`▓ŅŠ∙▓╗│¼▀^2ŅwŻ¼ätšJ(r©©n)×ķĄ├ĄĮĄ─ŠĆąį╗žÜwĘĮ│╠╩Ū┐╔┐┐Ą─Ż¼įćå¢Ż©1Ż®ųą╦∙Ą├Ą─ŠĆąį╗žÜwĘĮ│╠╩Ūʱ┐╔┐┐Ż┐
ūóŻ║ Ż¼
Ż¼![]() Ż«
Ż«
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐ęčų¬ČÓ├µ¾w![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Š∙┤╣ų▒ė┌ŲĮ├µ
Š∙┤╣ų▒ė┌ŲĮ├µ![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż«
Ż«

Ż©1Ż®ūC├„Ż║![]() Ī═ŲĮ├µ
Ī═ŲĮ├µ![]() Ż╗
Ż╗
Ż©2Ż®Ū¾ų▒ŠĆ![]() ┼cŲĮ├µ
┼cŲĮ├µ![]() ╦∙│╔Ą─ĮŪĄ─š²ŽęųĄŻ«
╦∙│╔Ą─ĮŪĄ─š²ŽęųĄŻ«
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐Ū¾ØMūŃŽ┬┴ąŚl╝■Ą─Ū·ŠĆĄ─ĘĮ│╠Ż║
Ż©1Ż®ļxą─┬╩×ķ![]() Ż¼ķL▌SķL×ķ6Ą─ÖEłAĄ─ś╦(bi©Īo)£╩(zh©│n)ĘĮ│╠
Ż¼ķL▌SķL×ķ6Ą─ÖEłAĄ─ś╦(bi©Īo)£╩(zh©│n)ĘĮ│╠
Ż©2Ż®┼cÖEłA![]() ėąŽÓ═¼Į╣³c(di©Żn)Ż¼ŪęĮø(j©®ng)▀^³c(di©Żn)
ėąŽÓ═¼Į╣³c(di©Żn)Ż¼ŪęĮø(j©®ng)▀^³c(di©Żn)![]() Ą─ļpŪ·ŠĆĄ─ś╦(bi©Īo)£╩(zh©│n)ĘĮ│╠Ż«
Ą─ļpŪ·ŠĆĄ─ś╦(bi©Īo)£╩(zh©│n)ĘĮ│╠Ż«
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐Ė─Ė’ķ_Ę┼ęįüĒŻ¼╬ęć°Įø(j©®ng)Ø·(j©¼)│ų└m(x©┤)Ė▀╦┘į÷ķL![]() ╚ńłDĮo│÷┴╦╬ęć°2003─Ļų┴2012─ĻĄ┌Č■«a(ch©Żn)śI(y©©)į÷╝ėųĄ┼cĄ┌ę╗«a(ch©Żn)śI(y©©)į÷╝ėųĄĄ─▓ŅųĄ
╚ńłDĮo│÷┴╦╬ęć°2003─Ļų┴2012─ĻĄ┌Č■«a(ch©Żn)śI(y©©)į÷╝ėųĄ┼cĄ┌ę╗«a(ch©Żn)śI(y©©)į÷╝ėųĄĄ─▓ŅųĄ![]() ęįŽ┬║åĘQ×ķŻ║«a(ch©Żn)śI(y©©)▓ŅųĄ
ęįŽ┬║åĘQ×ķŻ║«a(ch©Żn)śI(y©©)▓ŅųĄ![]() Ą─š█ŠĆłDŻ¼ėø«a(ch©Żn)śI(y©©)▓ŅųĄ×ķ
Ą─š█ŠĆłDŻ¼ėø«a(ch©Żn)śI(y©©)▓ŅųĄ×ķ![]() å╬╬╗Ż║╚fā|į¬
å╬╬╗Ż║╚fā|į¬![]() Ż«
Ż«
![]() Ū¾│÷yĻP(gu©Īn)ė┌─ĻĘ▌┤·┤atĄ─ŠĆąį╗žÜwĘĮ│╠Ż╗
Ū¾│÷yĻP(gu©Īn)ė┌─ĻĘ▌┤·┤atĄ─ŠĆąį╗žÜwĘĮ│╠Ż╗
![]() └¹ė├
└¹ė├![]() ųąĄ─╗žÜwĘĮ│╠Ż¼Ęų╬÷2003─Ļų┴2012─Ļ╬ęć°«a(ch©Żn)śI(y©©)▓ŅųĄĄ─ūā╗»ŪķørŻ¼▓óŅA(y©┤)£y╬ęć°«a(ch©Żn)śI(y©©)▓ŅųĄį┌──ę╗─Ļ╝s×ķ34╚fā|į¬Ż╗
ųąĄ─╗žÜwĘĮ│╠Ż¼Ęų╬÷2003─Ļų┴2012─Ļ╬ęć°«a(ch©Żn)śI(y©©)▓ŅųĄĄ─ūā╗»ŪķørŻ¼▓óŅA(y©┤)£y╬ęć°«a(ch©Żn)śI(y©©)▓ŅųĄį┌──ę╗─Ļ╝s×ķ34╚fā|į¬Ż╗
![]() ĮY(ji©”)║Žš█ŠĆłDŻ¼įćŪ¾│÷│²╚ź2007─Ļ«a(ch©Żn)śI(y©©)▓ŅųĄ║¾╩ŻėÓĄ─9─Ļ«a(ch©Żn)śI(y©©)▓ŅųĄĄ─ŲĮŠ∙ųĄ╝░ĘĮ▓Ņ
ĮY(ji©”)║Žš█ŠĆłDŻ¼įćŪ¾│÷│²╚ź2007─Ļ«a(ch©Żn)śI(y©©)▓ŅųĄ║¾╩ŻėÓĄ─9─Ļ«a(ch©Żn)śI(y©©)▓ŅųĄĄ─ŲĮŠ∙ųĄ╝░ĘĮ▓Ņ![]() ĮY(ji©”)╣¹Š½┤_ĄĮ
ĮY(ji©”)╣¹Š½┤_ĄĮ![]() Ż«
Ż«
ĖĮŻ║╗žÜwų▒ŠĆĄ─ą▒┬╩║═ĮžŠÓĄ─ūŅąĪČ■│╦Ę©╣└ėŗ(j©¼)╣½╩ĮĘųäe×ķŻ║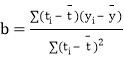 Ż¼
Ż¼![]() Ż«
Ż«
śė▒ŠĘĮ▓Ņ╣½╩ĮŻ║![]() Ż«
Ż«
ģó┐╝öĄ(sh©┤)ō■(j©┤)Ż║![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż«
Ż«

▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐ęčų¬Ą╚▓ŅöĄ(sh©┤)┴ą![]() Ū░5ĒŚ(xi©żng)║═×ķ50Ż¼
Ū░5ĒŚ(xi©żng)║═×ķ50Ż¼ ![]() Ż¼öĄ(sh©┤)┴ą
Ż¼öĄ(sh©┤)┴ą![]() Ą─Ū░
Ą─Ū░![]() ĒŚ(xi©żng)║═×ķ
ĒŚ(xi©żng)║═×ķ![]() Ż¼
Ż¼ ![]() Ż¼
Ż¼ ![]() .
.
Ż©ó±Ż®Ū¾öĄ(sh©┤)┴ą![]() Ż¼
Ż¼ ![]() Ą─═©ĒŚ(xi©żng)╣½╩ĮŻ╗
Ą─═©ĒŚ(xi©żng)╣½╩ĮŻ╗
Ż©ó“Ż®╚¶öĄ(sh©┤)┴ą![]() ØMūŃ
ØMūŃ![]() ,
, ![]() Ż¼Ū¾
Ż¼Ū¾![]() Ą─ųĄ.
Ą─ųĄ.
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐į┌ė╔öĄ(sh©┤)ūų1Ż¼2Ż¼3Ż¼4Ż¼5ĮM│╔Ą─╦∙ėąø]ėąųžÅ═(f©┤)öĄ(sh©┤)ūųĄ─╦─╬╗öĄ(sh©┤)ųąŻ¼┤¾ė┌3145ŪęąĪė┌4231Ą─öĄ(sh©┤)╣▓ėąŻ© Ż®
A.27éĆ(g©©)B.28éĆ(g©©)C.29éĆ(g©©)D.30éĆ(g©©)
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐öĄ(sh©┤)┴ą![]() ØMūŃ
ØMūŃ![]() ī”(du©¼)╚╬ęŌĄ─
ī”(du©¼)╚╬ęŌĄ─![]() ║Ń│╔┴óŻ¼
║Ń│╔┴óŻ¼![]() ×ķŲõŪ░
×ķŲõŪ░![]() ĒŚ(xi©żng)Ą─║═Ż¼Ūę
ĒŚ(xi©żng)Ą─║═Ż¼Ūę![]() Ż«
Ż«
Ż©1Ż®Ū¾öĄ(sh©┤)┴ą![]() Ą─═©ĒŚ(xi©żng)
Ą─═©ĒŚ(xi©żng)![]() Ż╗
Ż╗
Ż©2Ż®öĄ(sh©┤)┴ą![]() ØMūŃ
ØMūŃ![]() Ż¼Ųõųą
Ż¼Ųõųą![]() Ż«
Ż«
ó┘ūC├„Ż║öĄ(sh©┤)┴ą![]() ×ķĄ╚▒╚öĄ(sh©┤)┴ąŻ╗
×ķĄ╚▒╚öĄ(sh©┤)┴ąŻ╗
ó┌Ū¾╝»║Ž![]() Ż«
Ż«
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
ć°ļHīW(xu©”)ąŻā×(y©Łu)▀x - ŠÜ┴Ģ(x©¬)āį┴ą▒Ē - įćŅ}┴ą▒Ē
║■▒▒╩Ī╗ź┬ō(li©ón)ŠW(w©Żng)▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾(b©żo)ŲĮ┼_(t©ói) | ŠW(w©Żng)╔Žėą║”ą┼Žó┼eł¾(b©żo)īŻģ^(q©▒) | ļŖą┼įp“_┼eł¾(b©żo)īŻģ^(q©▒) | ╔µÜv╩Ę╠ō¤oų„┴xėą║”ą┼Žó┼eł¾(b©żo)īŻģ^(q©▒) | ╔µŲ¾ŪųÖÓ(qu©ón)┼eł¾(b©żo)īŻģ^(q©▒)
▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾(b©żo)ļŖįÆŻ║027-86699610 ┼eł¾(b©żo)Ó]ŽõŻ║58377363@163.com