
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若![]() ,求函數
,求函數![]() 的單調區間;
的單調區間;
(3)若函數![]() 有兩個極值點
有兩個極值點![]() ,若過兩點
,若過兩點![]() 的直線
的直線![]() 與
與![]() 軸的交點在曲線
軸的交點在曲線![]() 上,求
上,求![]() 的值.
的值.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)當![]() 時,求得
時,求得![]() ,解得
,解得![]() ,
,![]() ,利用導數的幾何意義,即可求解,得到答案.
,利用導數的幾何意義,即可求解,得到答案.
(2)求得![]() ,由
,由![]() ,解得
,解得![]() ,
,![]() ,分類討論,求得即可得到函數的單調性;
,分類討論,求得即可得到函數的單調性;
(3)求得![]() ,由
,由![]() 為方程
為方程![]() 的兩個根,求得
的兩個根,求得![]() 及
及![]() ,進而求得
,進而求得![]() ,
,![]() ,得出兩點
,得出兩點![]() 在直線
在直線![]() 上,求得
上,求得![]() 與
與![]() 軸的交點為
軸的交點為![]() ,代入
,代入![]() ,即可求解.
,即可求解.
(1)由題意,當![]() 時,
時,![]() ,則
,則![]() ,可得
,可得![]() ,
,![]() ,
,
所以點![]() 處的切線方程為
處的切線方程為![]() ,即
,即![]() .
.
(2)由題意,得![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
①當![]() 時,
時,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上單增;
上單增;
②當![]() 時,
時,![]() .
.
|
|
|
|
|
|
| + | 0 | — | 0 | + |
| ↑ | 極大值 | ↓ | 極小值 | ↑ |
所以![]() 單增區間為
單增區間為![]() 和
和![]() ,單減區間為
,單減區間為![]() .
.
(3)由函數![]() ,則
,則![]() ,
,
由題設知![]() 為方程
為方程![]() 的兩個根,故有
的兩個根,故有![]() ,解得
,解得![]()
且![]()
![]()
![]() ,
,
同理![]() ,
,
所以兩點![]() 在直線
在直線![]() 上,
上,
設![]() 與
與![]() 軸的交點為
軸的交點為![]() ,得
,得![]() ,
,
由題設,點![]() 在曲線
在曲線![]() 上,
上,
所以![]()
解得![]() 或
或![]() 或
或![]() ,所以
,所以![]() 的值為
的值為![]() 或
或![]() 或
或![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】設拋物線C:y2=4x的焦點為F,過F的直線l與C交于A,B兩點,點M的坐標為(﹣1,0).
(1)當l與x軸垂直時,求△ABM的外接圓方程;
(2)記△AMF的面積為S1,△BMF的面積為S2,當S1=4S2時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年,在慶祝中華人民共和國成立
年,在慶祝中華人民共和國成立![]() 周年之際,又迎來了以“創軍人榮耀,筑世界和平”為宗旨的第七屆世界軍人運動會.據悉,這次軍運會將于
周年之際,又迎來了以“創軍人榮耀,筑世界和平”為宗旨的第七屆世界軍人運動會.據悉,這次軍運會將于![]() 年
年![]() 月
月![]() 日至
日至![]() 日在美麗的江城武漢舉行,屆時將有來自全世界
日在美麗的江城武漢舉行,屆時將有來自全世界![]() 多個國家和地區的近萬名軍人運動員參賽.相對于奧運會、亞運會等大型綜合賽事,軍運會或許對很多人來說還很陌生.為此,武漢某高校為了在學生中更廣泛的推介普及軍運會相關知識內容,特在網絡上組織了一次“我所知曉的武漢軍運會”知識問答比賽,為便于對答卷進行對比研究,組委會抽取了
多個國家和地區的近萬名軍人運動員參賽.相對于奧運會、亞運會等大型綜合賽事,軍運會或許對很多人來說還很陌生.為此,武漢某高校為了在學生中更廣泛的推介普及軍運會相關知識內容,特在網絡上組織了一次“我所知曉的武漢軍運會”知識問答比賽,為便于對答卷進行對比研究,組委會抽取了![]() 名男生和
名男生和![]() 名女生的答卷,他們的考試成績頻率分布直方圖如下:
名女生的答卷,他們的考試成績頻率分布直方圖如下:
(注:問卷滿分為![]() 分,成績
分,成績![]() 的試卷為“優秀”等級)
的試卷為“優秀”等級)
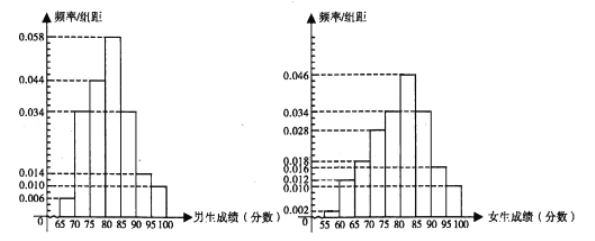
(1)從現有![]() 名男生和
名男生和![]() 名女生答卷中各取一份,分別求答卷成績為“優秀”等級的概率;
名女生答卷中各取一份,分別求答卷成績為“優秀”等級的概率;
(2)求列聯表中![]() ,
,![]() ,
,![]() ,
,![]() 的值,并根據列聯表回答:能否在犯錯誤的概率不超過
的值,并根據列聯表回答:能否在犯錯誤的概率不超過![]() 的前提下認為“答卷成績為優秀等級與性別有關”?
的前提下認為“答卷成績為優秀等級與性別有關”?
男 | 女 | 總計 | |
優秀 |
|
|
|
非優秀 |
|
|
|
總計 |
|
|
|
(3)根據男、女生成績頻率分布直方圖,對他們的成績的優劣進行比較.
附:參考公式:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(請寫出式子在寫計算結果)有4個不同的小球,4個不同的盒子,現在要把球全部放入盒內:
(1)共有多少種方法?
(2)若每個盒子不空,共有多少種不同的方法?
(3)恰有一個盒子不放球,共有多少種放法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對在直角坐標系的第一象限內的任意兩點![]() ,
,![]() 作如下定義:
作如下定義:![]() ,那么稱點
,那么稱點![]() 是點
是點![]() 的“上位點”,同時點
的“上位點”,同時點![]() 是點
是點![]() 的“下位點”.
的“下位點”.
(1)試寫出點![]() 的一個“上位點”坐標和一個“下位點”坐標;
的一個“上位點”坐標和一個“下位點”坐標;
(2)設![]() 、
、![]() 、
、![]() 、
、![]() 均為正數,且點
均為正數,且點![]() 是點
是點![]() 的上位點,請判斷點
的上位點,請判斷點![]() 是否既是點
是否既是點![]() 的“下位點”又是點
的“下位點”又是點![]() 的“上位點”,如果是請證明,如果不是請說明理由;
的“上位點”,如果是請證明,如果不是請說明理由;
(3)設正整數![]() 滿足以下條件:對任意實數
滿足以下條件:對任意實數![]() ,總存在
,總存在![]() ,使得點
,使得點![]() 既是點
既是點![]() 的“下位點”,又是點
的“下位點”,又是點![]() 的“上位點”,求正整數
的“上位點”,求正整數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與圓
與圓![]() :
:![]() 有且僅有兩個公共點,點
有且僅有兩個公共點,點![]() 、
、![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 上的動點、左焦點、右焦點,三角形
上的動點、左焦點、右焦點,三角形![]() 面積的最大值是
面積的最大值是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 在橢圓第一象限部分上運動,過點
在橢圓第一象限部分上運動,過點![]() 作圓
作圓![]() 的切線
的切線![]() ,過點
,過點![]() 作
作![]() 的垂線
的垂線![]() ,求證:
,求證:![]() ,
,![]() 交點
交點![]() 的縱坐標的絕對值為定值.
的縱坐標的絕對值為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com