
【題目】2018年4月4日召開的國務院常務會議明確將進一步推動網絡提速降費工作落實,推動我國數字經濟發展和信息消費,今年移動流量資費將再降![]() 以上,為響應國家政策,某通訊商計劃推出兩款優惠流量套餐,詳情如下:
以上,為響應國家政策,某通訊商計劃推出兩款優惠流量套餐,詳情如下:
套餐名稱 | 月套餐費/元 | 月套餐流量/M |
A | 30 | 3000 |
B | 50 | 6000 |
這兩款套餐均有以下附加條款:套餐費用月初一次性收取,手機使用流量一旦超出套餐流量,系統就會自動幫用戶充值![]() 流量,資費20元;如果又超出充值流量,系統再次自動幫用戶充值
流量,資費20元;如果又超出充值流量,系統再次自動幫用戶充值![]() 流量,資費20元,以此類推.此外,若當月流量有剩余,系統將自動清零,不可次月使用.
流量,資費20元,以此類推.此外,若當月流量有剩余,系統將自動清零,不可次月使用.
小張過去50個月的手機月使用流量(單位:M)的頻數分布表如下:
月使用流量分組 |
|
|
|
|
|
|
頻數 | 4 | 5 | 11 | 16 | 12 | 2 |
根據小張過去50個月的手機月使用流量情況,回答以下幾個問題:
(1)若小張選擇A套餐,將以上頻率作為概率,求小張在某一個月流量費用超過50元的概率;
(2)小張擬從A或B套餐中選定一款,若以月平均費用作為決策依據,他應訂哪一種套餐?說明理由.
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)求函數f(x)的定義域,判斷并證明函數f(x)的奇偶性;
(Ⅱ)是否存在這樣的實數k,使f(k-x2)+f(2k-x4)≥0對一切![]() 恒成立,若存在,試求出k的取值集合;若不存在,請說明理由.
恒成立,若存在,試求出k的取值集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新個稅法于2019年1月1日進行實施.為了調查國企員工對新個稅法的滿意程度,研究人員在![]() 地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布直方圖,其中
地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布直方圖,其中![]() .
.
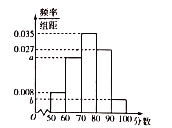
(1)求![]() 的值并估計被調查的員工的滿意程度的中位數;(計算結果保留兩位小數)
的值并估計被調查的員工的滿意程度的中位數;(計算結果保留兩位小數)
(2)若按照分層抽樣從![]() ,
,![]() 中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在
中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分形理論是當今世界十分風靡和活躍的新理論、新學科。其中,把部分與整體以某種方式相似的形體稱為分形。分形是一種具有自相似特性的現象,圖象或者物理過程。標準的自相似分形是數學上的抽象,迭代生成無限精細的結構。也就是說,在分形中,每一組成部分都在特征上和整體相似,只僅僅是變小了一些而已,謝爾賓斯基三角形就是一種典型的分形,是由波蘭數學家謝爾賓斯基在1915年提出的,按照如下規律依次在一個黑色三角形內去掉小三角形則當![]() 時,該黑色三角形內共去掉( )個小三角形
時,該黑色三角形內共去掉( )個小三角形
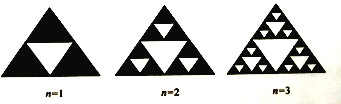
A. 81 B. 121 C. 364 D. 1093
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)求函數![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .(Ⅱ)當
.(Ⅱ)當![]() 時,
時, ![]()
![]() ;當
;當![]() 時,
時, ![]()
![]() .
.
【解析】【試題分析】(I)利用![]() 的二階導數來研究求得函數
的二階導數來研究求得函數![]() 的單調區間.(II) 由(Ⅰ)得
的單調區間.(II) 由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,由此可知
上單調遞增,由此可知![]() .利用導數和對
.利用導數和對![]() 分類討論求得函數在
分類討論求得函數在![]() 不同取值時的最大值.
不同取值時的最大值.
【試題解析】
(Ⅰ)![]() ,
,
設![]()
![]() ,則
,則![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
從而得![]() 在
在![]() 上單調遞增,又∵
上單調遞增,又∵![]() ,
,
∴當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
因此, ![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
(Ⅱ)由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
由此可知![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
設![]() ,
,
則![]()
![]()
 .
.
∵當![]() 時,
時, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
又∵![]() ,∴當
,∴當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
①當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() ;
;
②當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() .
.
綜上, ![]() 在
在![]() 上的最大值為:當
上的最大值為:當![]() 時,
時, ![]()
![]() ;
;
當![]() 時,
時, ![]()
![]() .
.
[點睛]本小題主要考查函數的單調性,考查利用導數求最大值. 與函數零點有關的參數范圍問題,往往利用導數研究函數的單調區間和極值點,并結合特殊點,從而判斷函數的大致圖像,討論其圖象與![]() 軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
【題型】解答題
【結束】
22
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,圓
中,圓![]() 的普通方程為
的普通方程為![]() . 在以坐標原點為極點,
. 在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ) 寫出圓 ![]() 的參數方程和直線
的參數方程和直線![]() 的直角坐標方程;
的直角坐標方程;
( Ⅱ ) 設直線![]() 與
與![]() 軸和
軸和![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() 為圓
為圓![]() 上的任意一點,求
上的任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,雙十一購物狂歡節(簡稱“雙11”)活動已成為中國電子商務行業年度盛事,某網絡商家為制定2018年“雙11”活動營銷策略,調查了2017年“雙11”活動期間每位網購客戶用于網購時間![]() (單位:小時),發現
(單位:小時),發現![]() 近似服從正態分布
近似服從正態分布![]() .
.
(1)求![]() 的估計值;
的估計值;
(2)該商家隨機抽取參與2017年“雙11”活動的10000名網購客戶,這10000名客戶在2017年“雙11”活動期間,用于網購時間![]() 屬于區間
屬于區間![]() 的客戶數為
的客戶數為![]() .該商家計劃在2018年“雙11”活動前對這
.該商家計劃在2018年“雙11”活動前對這![]() 名客戶發送廣告,所發廣告的費用為每位客戶0.05元.
名客戶發送廣告,所發廣告的費用為每位客戶0.05元.
(i)求該商家所發廣告總費用的平均估計值;
(ii)求使![]() 取最大值時的整數
取最大值時的整數![]() 的值.
的值.
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為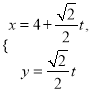 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的非負半軸為極軸建立極坐標系,圓
軸的非負半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(1)求圓![]() 的直角坐標方程及弦
的直角坐標方程及弦![]() 的長;
的長;
(2)動點![]() 在圓
在圓![]() 上(不與
上(不與![]() ,
, ![]() 重合),試求
重合),試求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com