
【題目】已知數列![]() 的首項為
的首項為![]() ,前
,前![]() 項和為
項和為![]() 與
與![]() 之間滿足
之間滿足![]()
![]() ,
,
(Ⅰ)求證:數列![]() 是等差數列;
是等差數列;
(Ⅱ)求數列![]() 的通項公式;
的通項公式;
(Ⅲ)設存在正整數![]() ,使
,使![]() 對一切
對一切![]() 都成立,求
都成立,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)見解析.(Ⅱ)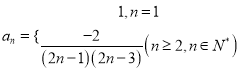 (Ⅲ)
(Ⅲ)![]() .
.
【解析】試題分析:(Ⅰ)數列{an}的前n項和Sn與an之間滿足an=![]()
![]() ,化為
,化為![]()
![]() ,即可證明.(Ⅱ)由(Ⅰ)知,
,即可證明.(Ⅱ)由(Ⅰ)知, ![]() , 所以
, 所以![]()
![]() ,n≥2時,an=Sn-Sn-1;n=1時,a1=1.可得數列
,n≥2時,an=Sn-Sn-1;n=1時,a1=1.可得數列![]() 的通項公式;(Ⅲ)原不等式等價于
的通項公式;(Ⅲ)原不等式等價于![]() 對一切
對一切![]() 都成立,即
都成立,即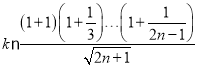 ,令
,令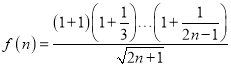 ,于是,
,于是, ![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]() ,即可解得正整數
,即可解得正整數![]() 的最大值.
的最大值.
試題解析:
(Ⅰ)因為![]()
![]() ,
,
故![]() ,
,
所以![]() ,
,
由題, ![]() ,兩邊同時除以
,兩邊同時除以![]() ,得
,得![]() ,
,
故![]()
![]() ,
,
故數列![]() 是公差為
是公差為![]() 的等差數列.
的等差數列.
(Ⅱ)由(Ⅰ)知, ![]() ,
,
所以![]()
![]() ,
,
![]()
![]() ,
,
又![]() ,不滿足上式,
,不滿足上式,
故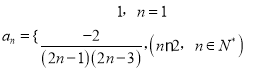 .
.
(Ⅲ)原不等式等價于![]() 對一切
對一切![]() 都成立,
都成立,
即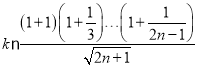 ,
,
令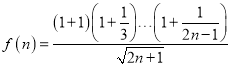 ,
,
于是, ![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]() ,
,
因為![]() 為正整數,所以
為正整數,所以![]() 的最大值為
的最大值為![]() .
.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
【題目】下列四個命題:
①樣本方差反映的是所有樣本數據與樣本平均值的偏離程度;
②基本事件空間是Ω={1,2,3,4,5,6},若事件A={1,3},B={3,5,6},A,B為互斥事件,但不是對立事件;
③某校高三(1)班和高三(2)班的人數分別是m,n,若一模考試數學平均分分別是a,b,則這兩個班的數學平均分為![]() ;
;
④如果平面外的一條直線上有兩個點到這個平面的距離相等,那么這條直線與這個平面的位置關系為平行或相交。
其中真命題的序號是__________。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱臺ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 
(1)求證:BC1⊥平面AA1C1C
(2)點D是B1C1的中點,求二面角A1﹣BD﹣B1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,且點
,且點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓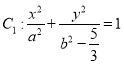 上異于其頂點的任意一點
上異于其頂點的任意一點![]() 作圓
作圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() (
(![]() 不在坐標軸上),若直線
不在坐標軸上),若直線![]() 在
在![]() 軸,
軸, ![]() 軸上的截距分別為
軸上的截距分別為![]() ,證明:
,證明: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠在政府的幫扶下,準備轉型生產一種特殊機器,生產需要投入固定成本![]() 萬元,生產與銷售均已百臺計數,且每生產
萬元,生產與銷售均已百臺計數,且每生產![]() 臺,還需增加可變成本
臺,還需增加可變成本![]() 萬元,若市場對該產品的年需求量為
萬元,若市場對該產品的年需求量為![]() 臺,每生產
臺,每生產![]() 百臺的實際銷售收入近似滿足函數
百臺的實際銷售收入近似滿足函數![]() .
.
(![]() )試寫出第一年的銷售利潤
)試寫出第一年的銷售利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (單位:百臺,
(單位:百臺,![]() ,
,![]() )的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
)的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
(![]() )因技術等原因,第一年的年生產量不能超過
)因技術等原因,第一年的年生產量不能超過![]() 臺,若第一年的年支出費用
臺,若第一年的年支出費用![]() (萬元)與年產量
(萬元)與年產量![]() (百臺)的關系滿足
(百臺)的關系滿足![]() ,問年產量
,問年產量![]() 為多少百臺時,工廠所得純利潤最大?
為多少百臺時,工廠所得純利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:集合![]() ,其中
,其中
![]() .
.![]() ,稱
,稱![]() 為
為![]() 的第
的第![]() 個坐標分量.若
個坐標分量.若![]() ,且滿足如下兩條性質:
,且滿足如下兩條性質:
①![]() 中元素個數不少于
中元素個數不少于![]() 個.
個.
②![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 的第
的第![]() 個坐標分量都是
個坐標分量都是![]() .則稱
.則稱![]() 為
為![]() 的一個好子集.
的一個好子集.
(![]() )若
)若![]() 為
為![]() 的一個好子集,且
的一個好子集,且![]() ,
,![]() ,寫出
,寫出![]() ,
,![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集,求證:
的一個好子集,求證:![]() 中元素個數不超過
中元素個數不超過![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集且
的一個好子集且![]() 中恰好有
中恰好有![]() 個元素,求證:一定存在唯一一個
個元素,求證:一定存在唯一一個![]() ,使得
,使得![]() 中所有元素的第
中所有元素的第![]() 個坐標分量都是
個坐標分量都是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某校參加高二年級學業水平考試模擬考試的學生中抽取60名學生,將其數學成績分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,畫出如圖的頻率分布直方圖.根據圖形信息,解答下列問題:
(1)估計這次考試成績的眾數,中位數,平均數;
(2)估計這次考試成績的及格率(60分及其以上為及格).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com