
【題目】已知函數(shù)y=f(x)=-x3+ax2+b(a,b∈R).
(1)當(dāng)a>0時(shí),若f(x)滿足:y極小值=1,y極大值=![]() ,試求f(x)的解析式;
,試求f(x)的解析式;
(2)若x∈[0,1]時(shí),y=f(x)圖象上的任意一點(diǎn)處的切線斜率k滿足:|k|≤1,求a的取值范圍.
【答案】(1)f(x)=-x3+x2+1;(2)![]()
【解析】
(1)由![]() (x)=-3x2+2ax=0得x=0或x=
(x)=-3x2+2ax=0得x=0或x=![]() ,易求出函數(shù)取極值時(shí)x的值,然后根據(jù)函數(shù)f(x)的極小值和極大值分別為1、
,易求出函數(shù)取極值時(shí)x的值,然后根據(jù)函數(shù)f(x)的極小值和極大值分別為1、![]() ,構(gòu)造關(guān)于a,b的方程,解方程后即可求出函數(shù)y=f(x)的解析式;(2)根據(jù)導(dǎo)數(shù)的幾何意義可知|k|=|f′(x)|≤1在x∈[0,1]恒成立,將a分離出來,使之恒成立即可求出a的范圍.
,構(gòu)造關(guān)于a,b的方程,解方程后即可求出函數(shù)y=f(x)的解析式;(2)根據(jù)導(dǎo)數(shù)的幾何意義可知|k|=|f′(x)|≤1在x∈[0,1]恒成立,將a分離出來,使之恒成立即可求出a的范圍.
(1)![]() (x)=-3x2+2ax=0得x=0或x=
(x)=-3x2+2ax=0得x=0或x=![]() .
.
a>0時(shí),x變化時(shí)f'(x),f(x)變化如下表:
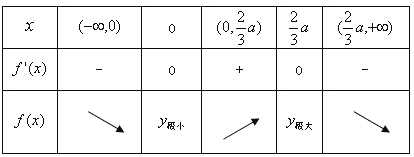
所以f(0)=b=1,![]() ,解得a=1,b=1.故f(x)=-x3+x2+1;
,解得a=1,b=1.故f(x)=-x3+x2+1;
(2)由題設(shè)x∈[0,1]時(shí),恒有|k|=|f′(x)|≤1,
即-1≤-3x2+2ax≤1在x∈[0,1]上恒成立.
當(dāng)x=0時(shí),a∈R;
當(dāng)x∈(0,1]時(shí),由-3x2+2ax≥-1恒成立,即2ax≥3x2-1,![]()
y=![]() 在(0,1]上為增函數(shù)
在(0,1]上為增函數(shù)
所以a≥1
另一方面,由-3x2+2ax≤1恒成立,![]() 所以
所以![]() (當(dāng)且僅當(dāng)x=
(當(dāng)且僅當(dāng)x=![]() 時(shí),取最值).
時(shí),取最值).
綜上所述:![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)等差數(shù)列{an}的前n項(xiàng)和為Sn,若S9=81,a3+a5=14.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)bn=![]() ,若{bn}的前n項(xiàng)和為Tn,證明:Tn<
,若{bn}的前n項(xiàng)和為Tn,證明:Tn<![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某船在海面![]() 處測(cè)得燈塔
處測(cè)得燈塔![]() 在北偏東
在北偏東![]() 方向,與
方向,與![]() 相距
相距![]() 海里,測(cè)得燈塔
海里,測(cè)得燈塔![]() 在北偏西
在北偏西![]() 方向,與
方向,與![]() 相距
相距![]() 海里,船由
海里,船由![]() 向正北方向航行到
向正北方向航行到![]() 處,測(cè)得燈塔
處,測(cè)得燈塔![]() 在南偏西
在南偏西![]() 方向,這時(shí)燈塔
方向,這時(shí)燈塔![]() 與
與![]() 相距多少海里?
相距多少海里?![]() 在
在![]() 的什么方向?
的什么方向?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
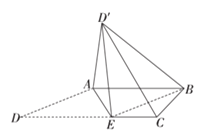
【題目】如圖所示,已知四邊形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,其中
,其中![]() 是
是![]() 上的一點(diǎn),四邊形
上的一點(diǎn),四邊形![]() 是菱形,滿足
是菱形,滿足![]() ,沿
,沿![]() 將
將![]() 折起,使
折起,使![]()
(1)求證:平面![]() 平面
平面![]()
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l1:x-2y+3=0與直線l2:2x+3y-8=0的交點(diǎn)為M,
(1)求過點(diǎn)M且到點(diǎn)P(0,4)的距離為2的直線l的方程;
(2)求過點(diǎn)M且與直線l3:x+3y+1=0平行的直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】唐三彩,中國(guó)古代陶瓷燒制工藝的珍品,它吸取了中國(guó)國(guó)畫、雕塑等工藝美術(shù)的特點(diǎn),在中國(guó)文化中占有重要的歷史地位,在中國(guó)的陶瓷史上留下了濃墨重彩的一筆.唐三彩的生產(chǎn)至今已有1300多年的歷史,對(duì)唐三彩的復(fù)制和仿制工藝,至今也有百余年的歷史,某陶瓷廠在生產(chǎn)過程中,對(duì)仿制100件工藝品測(cè)得其重量(單位:![]() ) 數(shù)據(jù),將數(shù)據(jù)分組如下表:
) 數(shù)據(jù),將數(shù)據(jù)分組如下表:

(1)統(tǒng)計(jì)方法中,同一組數(shù)據(jù)常用該組區(qū)間的中點(diǎn)值(例如區(qū)間![]() 的中點(diǎn)值是2.25)作為代表.據(jù)此,估計(jì)這100個(gè)數(shù)據(jù)的平均值;
的中點(diǎn)值是2.25)作為代表.據(jù)此,估計(jì)這100個(gè)數(shù)據(jù)的平均值;
(2)根據(jù)樣本數(shù)據(jù),以頻率作為槪率,若該陶瓷廠生產(chǎn)這樣的工藝品5000件,試估計(jì)重量落在![]() 中的件數(shù);
中的件數(shù);
(3)從第一組和第六組6件工藝品中隨機(jī)抽取2個(gè)工藝品,求一個(gè)來自第一組,一個(gè)來自第六組的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
已知曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() :
:![]() ,直線
,直線![]() :
:![]() .以極點(diǎn)
.以極點(diǎn)![]() 為原點(diǎn),極軸為
為原點(diǎn),極軸為![]() 軸的正半軸建立平面直角坐標(biāo)系.
軸的正半軸建立平面直角坐標(biāo)系.
(1)求直線![]() ,
,![]() 的直角坐標(biāo)方程以及曲線
的直角坐標(biāo)方程以及曲線![]() 的參數(shù)方程;
的參數(shù)方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點(diǎn),直線
兩點(diǎn),直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是異面直線,則以下四個(gè)命題:①存在分別經(jīng)過直線
是異面直線,則以下四個(gè)命題:①存在分別經(jīng)過直線![]() 和
和![]() 的兩個(gè)互相垂直的平面;②存在分別經(jīng)過直線
的兩個(gè)互相垂直的平面;②存在分別經(jīng)過直線![]() 和
和![]() 的兩個(gè)平行平面;③經(jīng)過直線
的兩個(gè)平行平面;③經(jīng)過直線![]() 有且只有一個(gè)平面垂直于直線
有且只有一個(gè)平面垂直于直線![]() ;④經(jīng)過直線
;④經(jīng)過直線![]() 有且只有一個(gè)平面平行于直線
有且只有一個(gè)平面平行于直線![]() ,其中正確的個(gè)數(shù)有( )
,其中正確的個(gè)數(shù)有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題正確的是
(1)命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l為直線,![]() ,
,![]() 為兩個(gè)不同的平面,若
為兩個(gè)不同的平面,若![]() ,
,![]() ,則
,則![]() ;
;
(3)給定命題p,q,若“![]() 為真命題”,則
為真命題”,則![]() 是假命題;
是假命題;
(4)“![]() ”是“
”是“![]() ”的充分不必要條件.
”的充分不必要條件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com