
【題目】【四川省高2017屆第一次名校聯考(廣志聯考)(理)】已知函數![]() .
.
(Ⅰ)當![]() 時,存在
時,存在![]() 使不等式
使不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若在區(qū)間![]() 上,函數
上,函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
【答案】(I)![]() ;(II)詳見解析.
;(II)詳見解析.
【解析】試題分析:
試題解析:(I)借助存在型不等式成立的條件建立不等式;(II)先建立不等式,再運用導數知識求解:
解:(Ⅰ)當![]() 時,
時,![]() ,
,
所以![]() ,由
,由![]() 知
知![]() ,
,
則函數![]() 在區(qū)間
在區(qū)間![]() 為增函數,
為增函數,
則當![]() 時,
時,![]() ,
,
故存在![]() 使不等式
使不等式![]() 成立,
成立,
只需![]() 即可.
即可.
(Ⅱ)在區(qū)間![]() 上,函數
上,函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的下方等價于對任意
的下方等價于對任意![]() ,
,![]() ,
,
即![]() 恒成立,
恒成立,
設![]() ,
,![]() .
.
則![]()
當![]() 時,
時,![]() ,
,![]() .
.
①若![]() ,即
,即![]() ,有
,有![]() ,
,
則函數![]() 在區(qū)間
在區(qū)間![]() 為減函數,
為減函數,
則對任意![]() ,
,![]() ,
,
只需![]() ,即當
,即當![]() 時,
時,![]() 恒成立.
恒成立.
②若![]() ,即
,即![]() 時,
時,
令![]() ,
,
得![]() .
.
則函數![]() 在區(qū)間
在區(qū)間![]() 為減函數,在區(qū)間
為減函數,在區(qū)間![]() 為增函數,
為增函數,
則![]() ,不合題意.
,不合題意.
③若![]() ,即當
,即當![]() 時,
時,![]() ,函數
,函數![]() 在區(qū)間
在區(qū)間![]() 為增函數,
為增函數,
則![]() ,不合題意.
,不合題意.
綜上,當![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 恒成立,
恒成立,
即當![]() 時,在區(qū)間
時,在區(qū)間![]() 上函數
上函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的下方.
的下方.


科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)若函數![]() 的圖象與x軸無交點,求a的取值范圍;
的圖象與x軸無交點,求a的取值范圍;
(2) 若函數![]() 在[-1,1]上存在零點,求a的取值范圍;
在[-1,1]上存在零點,求a的取值范圍;
(3)設函數![]() ,當
,當![]() 時,若對任意的
時,若對任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() ,求b的取值范圍.
,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 過橢圓
過橢圓![]() :
: ![]() (
(![]() )的短軸端點,
)的短軸端點, ![]() ,
, ![]() 分別是圓
分別是圓![]() 與橢圓
與橢圓![]() 上任意兩點,且線段
上任意兩點,且線段![]() 長度的最大值為3.
長度的最大值為3.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 作圓
作圓![]() 的一條切線交橢圓
的一條切線交橢圓![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)的最小值為1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在區(qū)間[2a,a+1]上不單調,求實數a的取值范圍;
(3)在區(qū)間[-1,1]上,y=f(x)的圖象恒在y=2x+2m+1的圖象上方,試確定實數m的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題P:函數![]() 是增函數,命題Q:
是增函數,命題Q:![]()
(1)寫出命題Q的否命題![]() ,并求出實數
,并求出實數![]() 的取值范圍,使得命題
的取值范圍,使得命題![]() 為真命題;
為真命題;
(2)如果![]() 是真命題,
是真命題,![]() 是假命題,求實數
是假命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面為矩形,D為
的底面為矩形,D為![]()
的中點,AC⊥平面BCC1B1.
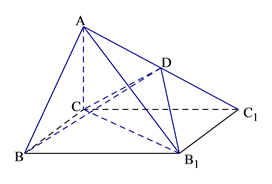
(Ⅰ)證明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的長;
(2)求三棱錐C-DB1C1的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節(jié)對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學舉辦安全法規(guī)知識競賽,從參賽的高一、高二學生中各抽出100人的成績作為樣本,對高一年級的100名學生的成績進行統計,并按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分組,得到成績分布的頻率分布直方圖(如圖)。
分組,得到成績分布的頻率分布直方圖(如圖)。

(1)若規(guī)定60分以上(包括60分)為合格,計算高一年級這次競賽的合格率;
(2)統計方法中,同一組數據常用該組區(qū)間的中點值作為代表,據此,估計高一年級這次知識競賽的學生的平均成績;
(3)若高二年級這次競賽的合格率為![]() ,由以上統計數據填寫下面
,由以上統計數據填寫下面![]() 列聯表,并問是否有
列聯表,并問是否有![]() 的把握認為“這次知識競賽的成績與年級有關”。
的把握認為“這次知識競賽的成績與年級有關”。
高一 | 高二 | 合計 | |
合格人數 | |||
不合格人數 | |||
合計 |
 附:參考數據與公式
附:參考數據與公式
高一 | 合計 | ||
合格人數 | a | b | a+b |
不合格人數 | c | d | c+d |
合計 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=3ax2+2bx+c,a+b+c=0,f(0)>0,f(1)>0,證明a>0,并利用二分法證明方程f(x)=0在區(qū)間[0,1]內有兩個實根.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com