

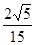 ;(3)
;(3)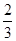 .
.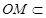 平面MBD,AN
平面MBD,AN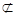 平面MBD
平面MBD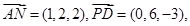
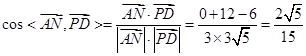
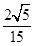
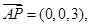
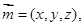
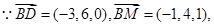 并且
并且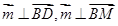
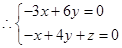 ,令y=1,得x=2,z=-2
,令y=1,得x=2,z=-2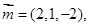
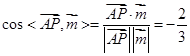
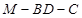 是銳角
是銳角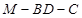 的余弦值為
的余弦值為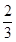 .
.

 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:高中數學 來源:不詳 題型:解答題
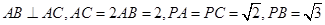 .
.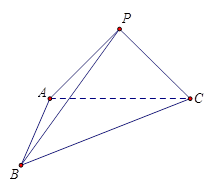
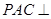 平面
平面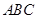 ;
;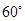 的角?若存在,求BQ的長;若不存在,請說明理由.
的角?若存在,求BQ的長;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.若a⊥α,b∥α,則a⊥b | B.若a⊥α,b∥a,b?β,則α⊥β |
| C.若a⊥α,b⊥β,α∥β,則a∥b | D.若a∥α,a∥β,則α∥β |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.①或② | B.②或③ | C.①或③ | D.② |
查看答案和解析>>