Question

（09年西城區(qū)抽樣理）（14分）

已知拋物線，點M(m,0)在x軸的正半軸上，過M的直線l與C相交于A、B兩點，O為坐標(biāo)原點.

（Ⅰ）若m=1，l的斜率為1，求以AB為直徑的圓的方程；

    （Ⅱ）若存在直線l使得成等比數(shù)列，求實數(shù)m的取值范圍.

Answer 1

 解析：（Ⅰ）解：由題意，得，直線l的方程為.

由, 得,

設(shè)A, B兩點坐標(biāo)為,  AB中點P的坐標(biāo)為,

則,

故點               ----------3分

所以,

故圓心為, 直徑,

所以以AB為直徑的圓的方程為；     -------------6分

方法一：（Ⅱ）解：設(shè)A, B兩點坐標(biāo)為, .

則,

      所以                     ①             

      因為點A, B在拋物線C上,

      所以,                     ②         

      由12，消去得.                        --------------10分

      若此直線l使得成等比數(shù)列，則，

      即，所以，

      因為，，所以，

整理得，             ③          -----------12分

      因為存在直線l使得成等比數(shù)列，

所以關(guān)于x₁的方程3有正根，

      因為方程3的兩根之積為m²>0, 所以只可能有兩個正根，

      所以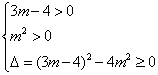，解得.

故當(dāng)時，存在直線l使得成等比數(shù)列.  ---------14分

方法二：（Ⅱ）解：設(shè)使得成等比數(shù)列的直線AB方程為或,

當(dāng)直線AB方程為時, ，

因為成等比數(shù)列,

所以，即，解得m=4，或m=0(舍)；-------8分

當(dāng)直線AB方程為時，

    由，得，

設(shè)A, B兩點坐標(biāo)為,

則,                         ① 

由m>0, 得.

因為成等比數(shù)列, 所以,

所以，               ②   

   因為A, B兩點在拋物線C上，

所以,                                 ③-----11分

   由①②③，消去,

得,

因為存在直線l使得成等比數(shù)列，

所以,

       綜上，當(dāng)時，存在直線l使得成等比數(shù)列.  -----14分