
【題目】己知函數(shù)![]() (其中e為自然對數(shù)的底數(shù)),
(其中e為自然對數(shù)的底數(shù)), ![]() .
.
(I)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)設(shè)![]() ,.已知直線
,.已知直線![]() 是曲線
是曲線![]() 的切線,且函數(shù)
的切線,且函數(shù)![]() 上是增函數(shù).
上是增函數(shù).
(i)求實數(shù)![]() 的值;
的值;
(ii)求實數(shù)c的取值范圍.
【答案】(I)見解析;(II)(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(I)求導(dǎo)得![]() ,討論
,討論![]() 和
和![]() 即可;
即可;
(II) (i)由相切得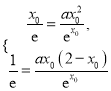 ,解方程即可;(ii)先構(gòu)造
,解方程即可;(ii)先構(gòu)造![]() 來討論
來討論![]() 和
和![]() 的大小,得
的大小,得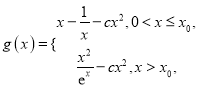 ,求導(dǎo),得
,求導(dǎo),得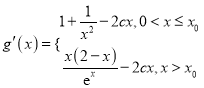 . 由函數(shù)
. 由函數(shù)![]() 在
在![]() 上是增函數(shù),且曲線
上是增函數(shù),且曲線![]() 在
在![]() 上連續(xù)不斷知:
上連續(xù)不斷知: ![]() 在
在![]() ,
, ![]() 上恒成立,分兩段討論即可.
上恒成立,分兩段討論即可.
試題解析:
(Ⅰ)∵![]() ,
,
∴![]() ,
,
①當(dāng)![]() 時,
時,
在![]() 時,
時, ![]() ,在
,在![]() 時,
時, ![]() ,
,
故![]() 在
在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù);
上是增函數(shù);
②當(dāng)![]() 時,
時,
在![]() 時,
時, ![]() ,在
,在![]() 時,
時, ![]() ,
,
故![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù);
上是減函數(shù);
(Ⅱ)(1)對![]() 求導(dǎo),得
求導(dǎo),得![]() ,
,
設(shè)直線![]() 與曲線
與曲線![]() 切于點
切于點![]() ,則
,則
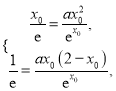 解得
解得![]() ,∴
,∴![]() ;
;
(2)記函數(shù)![]()
![]() ,
, ![]() ,
,
求導(dǎo),得![]() ,
,
當(dāng)![]() 時,
時, ![]() 恒成立,
恒成立,
當(dāng)![]() 時,
時, 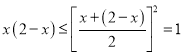 ,
,
∴![]()
![]() ,
,
∴![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上單調(diào)遞減.
上單調(diào)遞減.
又![]() ,
, ![]() ,
,
曲線![]() 在[1,2]上連續(xù)不間斷,
在[1,2]上連續(xù)不間斷,
∴由函數(shù)的零點存在性定理及其單調(diào)性知,唯一的![]() ∈(1,2),使
∈(1,2),使![]() .
.
∴當(dāng)![]() 時,
時, ![]() >0,當(dāng)
>0,當(dāng)![]() 時,
時, ![]() <0.
<0.
∴當(dāng)![]() 時,
時, ![]() =
=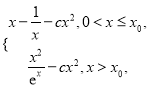
求導(dǎo),得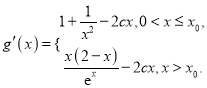
由函數(shù)![]() 在
在![]() 上是增函數(shù),且曲線
上是增函數(shù),且曲線![]() 在
在![]() 上連續(xù)不斷知:
上連續(xù)不斷知:
![]() 在
在![]() ,
, ![]() 上恒成立.
上恒成立.
①當(dāng)![]() 時,
時, ![]() ≥0在
≥0在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
記![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
,
當(dāng) ![]() 變化時,
變化時, ![]() ,
, ![]() 變化情況列表如下:
變化情況列表如下:
|
| 3 |
|
|
| 0 |
|
|
| 極小值 |
|
∴![]() min=
min= ![]() 極小值=
極小值= ![]()
![]() ,
,
故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() ,即
,即![]() .
.
②當(dāng)![]() 時,
時, ![]()
![]() ,
,
當(dāng)![]() 時,
時, ![]() 在
在![]() 上恒成立,
上恒成立,
綜合①②知,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上是增函數(shù).
上是增函數(shù).
故實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知經(jīng)銷某種商品的電商在任何一個銷售季度內(nèi),每售出![]() 噸該商品可獲利潤
噸該商品可獲利潤![]() 萬元,未售出的商品,每
萬元,未售出的商品,每![]() 噸虧損
噸虧損![]() 萬元.根據(jù)往年的銷售經(jīng)驗,得到一個銷售季度內(nèi)市場需求量的頻率分布直方圖如右圖所示.已知電商為下一個銷售季度籌備了
萬元.根據(jù)往年的銷售經(jīng)驗,得到一個銷售季度內(nèi)市場需求量的頻率分布直方圖如右圖所示.已知電商為下一個銷售季度籌備了![]() 噸該商品.現(xiàn)以
噸該商品.現(xiàn)以![]() (單位:噸,
(單位:噸, ![]() )表示下一個銷售季度的市場需求量,
)表示下一個銷售季度的市場需求量, ![]() (單位:萬元)表示該電商下一個銷售季度內(nèi)經(jīng)銷該商品獲得的利潤.
(單位:萬元)表示該電商下一個銷售季度內(nèi)經(jīng)銷該商品獲得的利潤.
(Ⅰ)根據(jù)頻率分布直方圖,估計一個銷售季度內(nèi)市場需求量![]() 的平均數(shù)與中位數(shù)的大小;
的平均數(shù)與中位數(shù)的大小;
(Ⅱ)根據(jù)直方圖估計利潤![]() 不少于57萬元的概率.
不少于57萬元的概率.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在三棱錐P -ABC中,PA⊥底面ABC,∠BCA![]() 90°,AP
90°,AP![]() AC,點D,E分別在棱PB,PC上,且BC∥平面ADE.
AC,點D,E分別在棱PB,PC上,且BC∥平面ADE.

(Ⅰ)求證:DE⊥平面PAC;
(Ⅱ)若PC⊥AD,且三棱錐P-ABC的體積為8,求多面體ABCED的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】己知函數(shù)![]() ,
, ![]() .
.
(I)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)設(shè)![]() ,已知函數(shù)
,已知函數(shù)![]() 在
在![]() 上是增函數(shù).
上是增函數(shù).
(1)研究函數(shù)![]() 上零點的個數(shù);
上零點的個數(shù);
(ii)求實數(shù)c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知tanα, ![]() 是關(guān)于x的方程x2﹣kx+k2﹣3=0的兩實根,且3π<α<
是關(guān)于x的方程x2﹣kx+k2﹣3=0的兩實根,且3π<α< ![]() π,求cos(3π+α)﹣sin(π+α)的值.
π,求cos(3π+α)﹣sin(π+α)的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分) 某中學(xué)的環(huán)保社團(tuán)參照國家環(huán)境標(biāo)準(zhǔn)制定了該校所在區(qū)域空氣質(zhì)量指數(shù)與空氣質(zhì)量等級對應(yīng)關(guān)系如下表(假設(shè)該區(qū)域空氣質(zhì)量指數(shù)不會超過![]() ):
):
空氣質(zhì)量指數(shù) |
|
|
|
|
|
|
空氣質(zhì)量等級 |
|
|
|
|
|
|
該社團(tuán)將該校區(qū)在![]() 年
年![]() 天的空氣質(zhì)量指數(shù)監(jiān)測數(shù)據(jù)作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
天的空氣質(zhì)量指數(shù)監(jiān)測數(shù)據(jù)作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
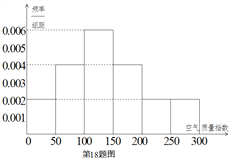
(Ⅰ)請估算![]() 年(以
年(以![]() 天計算)全年空氣質(zhì)量優(yōu)良的天數(shù)(未滿一天按一天計算);
天計算)全年空氣質(zhì)量優(yōu)良的天數(shù)(未滿一天按一天計算);
(Ⅱ)該校![]() 年
年![]() 月
月![]() 、
、![]() 日將作為高考考場,若這兩天中某天出現(xiàn)
日將作為高考考場,若這兩天中某天出現(xiàn)![]() 級重度污染,需要凈化空氣費用
級重度污染,需要凈化空氣費用![]() 元,出現(xiàn)
元,出現(xiàn)![]() 級嚴(yán)重污染,需要凈化空氣費用
級嚴(yán)重污染,需要凈化空氣費用![]() 元,記這兩天凈化空氣總費用為
元,記這兩天凈化空氣總費用為![]() 元,求
元,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
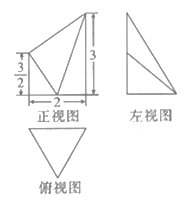
【題目】如圖,某幾何體的三視圖中,俯視圖是邊長為2的正三角形,正視圖和左視圖分別為直角梯形和直角三角形,則該幾何體的體積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com