
【題目】函數f(x)=Asin(ωx+φ)(ω>0, ![]() )的部分圖象如圖所示,將函數f(x)的圖象向右平移
)的部分圖象如圖所示,將函數f(x)的圖象向右平移 ![]() 個單位后得到函數g(x)的圖象,若函數g(x)在區間
個單位后得到函數g(x)的圖象,若函數g(x)在區間 ![]() (
( ![]() )上的值域為[﹣1,2],則θ= .
)上的值域為[﹣1,2],則θ= . 
【答案】![]()
【解析】解:根據函數f(x)=Asin(ωx+φ)(ω>0, ![]() )的部分圖象, 可得A=﹣2,
)的部分圖象, 可得A=﹣2, ![]() =
= ![]() =
= ![]() ,∴ω=2.
,∴ω=2.
再根據五點法作圖可得2 ![]() +φ=π,∴φ=
+φ=π,∴φ= ![]() ,f(x)=﹣2sin(2x+
,f(x)=﹣2sin(2x+ ![]() ).
).
將函數f(x)的圖象向右平移 ![]() 個單位后得到函數g(x)=﹣2sin(2x﹣
個單位后得到函數g(x)=﹣2sin(2x﹣ ![]() +
+ ![]() )=﹣2sin(2x﹣
)=﹣2sin(2x﹣ ![]() )的圖象,
)的圖象,
對于函數y=g(x),當x∈ ![]() (
( ![]() ),2x﹣
),2x﹣ ![]() ∈[﹣π,2θ﹣
∈[﹣π,2θ﹣ ![]() ],
],
由于g(x)的值域為[﹣1,2],故﹣2sin(2x﹣ ![]() )的最小值為﹣1,此時,2sin(2θ﹣
)的最小值為﹣1,此時,2sin(2θ﹣ ![]() )=
)= ![]() ,
,
則θ= ![]() ,
,
故答案為: ![]() .
.
由函數的最值求出A,由周期求出ω,由五點法作圖求出φ的值,可得f(x)的解析式.再利用y=Asin(ωx+φ)的圖象變換規律,求得g(x)的解析式,結合條件,利用正弦函數的定義域和值域,求得θ的值..


 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:
【題目】一種畫橢圓的工具如圖1所示.O是滑槽AB的中點,短桿ON可繞O轉動,長桿MN通過N處鉸鏈與ON連接,MN上的栓子D可沿滑槽AB滑動,且DN=ON=1,MN=3,當栓子D在滑槽AB內作往復運動時,帶動N繞O轉動,M處的筆尖畫出的橢圓記為C,以O為原點,AB所在的直線為x軸建立如圖2所示的平面直角坐標系. 
(1)求橢圓C的方程;
(2)設動直線l與兩定直線l1:x﹣2y=0和l2:x+2y=0分別交于P,Q兩點.若直線l總與橢圓C有且只有一個公共點,試探究:△OPQ的面積是否存在最小值?若存在,求出該最小值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sin(2x+
sin(2x+ ![]() )+sin2x.
)+sin2x.
(1)求函數f(x)的最小正周期;
(2)若函數g(x)對任意x∈R,有g(x)=f(x+ ![]() ),求函數g(x)在[﹣
),求函數g(x)在[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學著作《九章算術》有如下問題:“今有器中米,不知其數,前人取半,中人三分取一,后人四分取一,余米一斗五升.問,米幾何?”如圖是解決該問題的程序框圖,執行該程序框圖,若輸出的S=1.5(單位:升),則輸入k的值為( ) 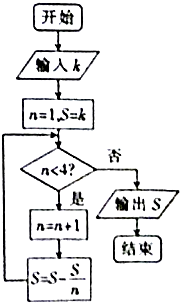
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A是拋物線y2=4x上的一點,以點A和點B(2,0)為直徑的圓C交直線x=1于M,N兩點.直線l與AB平行,且直線l交拋物線于P,Q兩點. (Ⅰ)求線段MN的長;
(Ⅱ)若 ![]() =﹣3,且直線PQ與圓C相交所得弦長與|MN|相等,求直線l的方程.
=﹣3,且直線PQ與圓C相交所得弦長與|MN|相等,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記f(n)為最接近 ![]() (n∈N*)的整數,如f(1)=1,f(2)=1,f(3)=2,f(4)=2,f(5)=2,…,若
(n∈N*)的整數,如f(1)=1,f(2)=1,f(3)=2,f(4)=2,f(5)=2,…,若 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =4054,則正整數m的值為( )
=4054,則正整數m的值為( )
A.2016×2017
B.20172
C.2017×2018
D.2018×2019
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體是由棱臺ABC﹣A1B1C1和棱錐D﹣AA1C1C拼接而成的組合體,其底面四邊形ABCD是邊長為2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2. 
(Ⅰ)求證:平面AB1C⊥平面BB1D;
(Ⅱ)求二面角A1﹣BD﹣C1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數,則f(x)=sin(2x+ ![]() )+cos(2x+
)+cos(2x+ ![]() ),則( )
),則( )
A.y=f(x)在(0, ![]() )單調遞增,其圖象關于直線x=
)單調遞增,其圖象關于直線x= ![]() 對稱
對稱
B.y=f(x)在(0, ![]() )單調遞增,其圖象關于直線x=
)單調遞增,其圖象關于直線x= ![]() 對稱
對稱
C.y=f(x)在(0, ![]() )單調遞減,其圖象關于直線x=
)單調遞減,其圖象關于直線x= ![]() 對稱
對稱
D.y=f(x)在(0, ![]() )單調遞減,其圖象關于直線x=
)單調遞減,其圖象關于直線x= ![]() 對稱
對稱
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com