
【題目】已知函數f(x)=x3+ax2+bx+1(a>0,b∈R)有極值,且導函數f′(x)的極值點是f(x)的零點.(極值點是指函數取極值時對應的自變量的值)
(Ⅰ)求b關于a的函數關系式,并寫出定義域;
(Ⅱ)證明:b2>3a;
(Ⅲ)若f(x),f′(x)這兩個函數的所有極值之和不小于﹣ ![]() ,求a的取值范圍.
,求a的取值范圍.
【答案】(Ⅰ)解:因為f(x)=x3+ax2+bx+1,
所以g(x)=f′(x)=3x2+2ax+b,g′(x)=6x+2a,
令g′(x)=0,解得x=﹣ ![]() .
.
由于當x>﹣ ![]() 時g′(x)>0,g(x)=f′(x)單調遞增;當x<﹣
時g′(x)>0,g(x)=f′(x)單調遞增;當x<﹣ ![]() 時g′(x)<0,g(x)=f′(x)單調遞減;
時g′(x)<0,g(x)=f′(x)單調遞減;
所以f′(x)的極小值點為x=﹣ ![]() ,
,
由于導函數f′(x)的極值點是原函數f(x)的零點,
所以f(﹣ ![]() )=0,即﹣
)=0,即﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +1=0,
+1=0,
所以b= ![]() +
+ ![]() (a>0).
(a>0).
因為f(x)=x3+ax2+bx+1(a>0,b∈R)有極值,
所以f′(x)=3x2+2ax+b=0有兩個不等的實根,
所以4a2﹣12b>0,即a2﹣ ![]() +
+ ![]() >0,解得a>3,
>0,解得a>3,
所以b= ![]() +
+ ![]() (a>3).
(a>3).
(Ⅱ)證明:由(1)可知h(a)=b2﹣3a= ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() (4a3﹣27)(a3﹣27),
(4a3﹣27)(a3﹣27),
由于a>3,所以h(a)>0,即b2>3a;
(Ⅲ)解:由(1)可知f′(x)的極小值為f′(﹣ ![]() )=b﹣
)=b﹣ ![]() ,
,
設x1 , x2是y=f(x)的兩個極值點,則x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
所以f(x1)+f(x2)= ![]() +
+ ![]() +a(
+a( ![]() +
+ ![]() )+b(x1+x2)+2
)+b(x1+x2)+2
=(x1+x2)[(x1+x2)2﹣3x1x2]+a[(x1+x2)2﹣2x1x2]+b(x1+x2)+2
= ![]() ﹣
﹣ ![]() +2,
+2,
又因為f(x),f′(x)這兩個函數的所有極值之和不小于﹣ ![]() ,
,
所以b﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +2=
+2= ![]() ﹣
﹣ ![]() ≥﹣
≥﹣ ![]() ,
,
因為a>3,所以2a3﹣63a﹣54≤0,
所以2a(a2﹣36)+9(a﹣6)≤0,
所以(a﹣6)(2a2+12a+9)≤0,
由于a>3時2a2+12a+9>0,
所以a﹣6≤0,解得a≤6,
所以a的取值范圍是(3,6].
【解析】(Ⅰ)通過對f(x)=x3+ax2+bx+1求導可知g(x)=f′(x)=3x2+2ax+b,進而再求導可知g′(x)=6x+2a,通過令g′(x)=0進而可知f′(x)的極小值點為x=﹣ ![]() ,從而f(﹣
,從而f(﹣ ![]() )=0,整理可知b=
)=0,整理可知b= ![]() +
+ ![]() (a>0),結合f(x)=x3+ax2+bx+1(a>0,b∈R)有極值可知f′(x)=0有兩個不等的實根,進而可知a>3.
(a>0),結合f(x)=x3+ax2+bx+1(a>0,b∈R)有極值可知f′(x)=0有兩個不等的實根,進而可知a>3.
(Ⅱ)通過(1)構造函數h(a)=b2﹣3a= ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() (4a3﹣27)(a3﹣27),結合a>3可知h(a)>0,從而可得結論;
(4a3﹣27)(a3﹣27),結合a>3可知h(a)>0,從而可得結論;
(Ⅲ)通過(1)可知f′(x)的極小值為f′(﹣ ![]() )=b﹣
)=b﹣ ![]() ,利用韋達定理及完全平方關系可知y=f(x)的兩個極值之和為
,利用韋達定理及完全平方關系可知y=f(x)的兩個極值之和為 ![]() ﹣
﹣ ![]() +2,進而問題轉化為解不等式b﹣
+2,進而問題轉化為解不等式b﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +2=
+2= ![]() ﹣
﹣ ![]() ≥﹣
≥﹣ ![]() ,因式分解即得結論.
,因式分解即得結論.
【考點精析】認真審題,首先需要了解基本求導法則(若兩個函數可導,則它們和、差、積、商必可導;若兩個函數均不可導,則它們的和、差、積、商不一定不可導),還要掌握利用導數研究函數的單調性(一般的,函數的單調性與其導數的正負有如下關系: 在某個區(qū)間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區(qū)間單調遞增;(2)如果
在這個區(qū)間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區(qū)間單調遞減)的相關知識才是答題的關鍵.
在這個區(qū)間單調遞減)的相關知識才是答題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D為AB的中點,AC=BC=BB1.

求證:(1)BC1⊥AB1.
(2)BC1∥平面CA1D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三名工人加工同一種零件,他們在一天中的工作情況如圖所示,其中Ai的橫、縱坐標分別為第i名工人上午的工作時間和加工的零件數,點Bi的橫、縱坐標分別為第i名工人下午的工作時間和加工的零件數,i=1,2,3.
①記Qi為第i名工人在這一天中加工的零件總數,則Q1 , Q2 , Q3中最大的是 .
②記pi為第i名工人在這一天中平均每小時加工的零件數,則p1 , p2 , p3中最大的是 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在R上且周期為1的函數,在區(qū)間[0,1)上,f(x)= ![]() ,其中集合D={x|x=
,其中集合D={x|x= ![]() ,n∈N*},則方程f(x)﹣lgx=0的解的個數是 .
,n∈N*},則方程f(x)﹣lgx=0的解的個數是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm,容器Ⅰ的底面對角線AC的長為10 ![]() cm,容器Ⅱ的兩底面對角線EG,E1G1的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
cm,容器Ⅱ的兩底面對角線EG,E1G1的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
(Ⅰ)將l放在容器Ⅰ中,l的一端置于點A處,另一端置于側棱CC1上,求l沒入水中部分的長度;
(Ⅱ)將l放在容器Ⅱ中,l的一端置于點E處,另一端置于側棱GG1上,求l沒入水中部分的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平行六面體ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ![]() ,∠BAD=120°.
,∠BAD=120°.
(Ⅰ)求異面直線A1B與AC1所成角的余弦值;
(Ⅱ)求二面角B﹣A1D﹣A的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,兩個頂點分別為
,兩個頂點分別為![]() ,
,![]() .過點
.過點![]() 的直線交橢圓于
的直線交橢圓于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與
與![]() 的交點為
的交點為![]() .
.
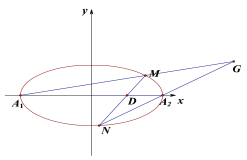
(1)求橢圓的標準方程;
(2)求證:點![]() 在一條定直線上.
在一條定直線上.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com