
【題目】在直角坐標系xoy中,直l線l的參數方程為 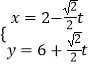 (t為參數).在極坐標系(與直角坐標系xoy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為ρ=10cosθ.
(t為參數).在極坐標系(與直角坐標系xoy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為ρ=10cosθ.
(1)求圓C的直角坐標方程;
(2)設圓C與直線l交于點A、B,若點P的坐標為(2,6),求|PA|+|PB|.
【答案】
(1)解:由ρ=10cosθ得ρ2=10ρcosθ,
∴直角坐標方程為:x2+y2=10x,配方為:(x﹣5)2+y2=25
(2)解:將l的參數方程代入圓C的直角坐標方程,化為 ![]() =0,
=0,
由于△= ![]() ﹣4×20=82>0,可設t1,t2是上述方程的兩個實根.
﹣4×20=82>0,可設t1,t2是上述方程的兩個實根.
∴t1+t2=﹣ ![]() ,t1t2=20,又直線l過點P(2,6),
,t1t2=20,又直線l過點P(2,6),
可得:|PA|+|PB|=|t1|+|t2|=﹣(t1+t2)=9 ![]()
【解析】(1)由ρ=10cosθ得ρ2=10ρcosθ,把 ![]() 代入即可得出.(2)將l的參數方程代入圓C的直角坐標方程,化為
代入即可得出.(2)將l的參數方程代入圓C的直角坐標方程,化為 ![]() =0,可設t1,t2是上述方程的兩個實根.利用|PA|+|PB|=|t1|+|t2|=﹣(t1+t2)即可得出.
=0,可設t1,t2是上述方程的兩個實根.利用|PA|+|PB|=|t1|+|t2|=﹣(t1+t2)即可得出.


科目:高中數學 來源: 題型:
【題目】在某校組織的一次籃球定點投籃訓練中,規定每人最多投3次;在A處每投進一球得3分,在B處每投進一球得2分;如果前兩次得分之和超過3分即停止投籃,否則投第三次,某同學在A處的命中率q1為0.25,在B處的命中率為q2 , 該同學選擇先在A處投一球,以后都在B處投,用ξ表示該同學投籃訓練結束后所得的總分,其分布列為:
ξ | 0 | 2 | 3 | 4 | 5 |
p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
(1)求q2的值;
(2)求隨機變量ξ的數學期望Eξ;
(3)試比較該同學選擇都在B處投籃得分超過3分與選擇上述方式投籃得分超過3分的概率的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為了對新研發的一種產品進行合理定價,隨機抽取了6個試銷售數據,得到第i個銷售單價xi(單位:元)與銷售yi(單位:件)的數據資料,算得 ![]()
(1)求回歸直線方程 ![]() ;
;
(2)預計在今后的銷售中,銷量與單價仍然服從(1)中的關系,且該產品的成本是4元/件,為使工廠獲得最大利潤,該產品的單價應定為多少元?(利潤=銷售收入﹣成本)
附:回歸直線方程 ![]() 中,
中, ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,其中
,其中 ![]() ,
, ![]() 是樣本平均值.
是樣本平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,記拋物線y=x﹣x2與x軸所圍成的平面區域為M,該拋物線與直線y=kx(k>0)所圍成的平面區域為N,向區域M內隨機拋擲一點P,若點P落在區域N內的概率為 ![]() ,則k的值為( )
,則k的值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接今年6月6日的“全國愛眼日”,某高中學校學生會隨機抽取16名學生,經校 醫用對數視力表檢查得到每個學生的視力狀況的莖葉圖(以小數點前的一位數字為莖,小數點后的一位數字為葉)如右圖,若視力測試結果不低于5.0,則稱為“好視力”, 
(1)寫出這組數據的眾數和中位數;
(2)求從這16人中隨機選取3人,至少有2人是“好視力”的概率;
(3)以這16人的樣本數據來估計整個學校的總體數據,若從該校(人數很多)任選3人,記X表示抽到“好視力”學生的人數,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在R上的偶函數,且f(2+x)=f(2﹣x),當x∈[﹣2,0]時,f(x)=( ![]() )x﹣1,若在區間(﹣2,6)內關于x的方程f(x)﹣log a(x+2)=0,恰有4個不同的實數根,則實數a(a>0,a≠1)的取值范圍是( )
)x﹣1,若在區間(﹣2,6)內關于x的方程f(x)﹣log a(x+2)=0,恰有4個不同的實數根,則實數a(a>0,a≠1)的取值范圍是( )
A.( ![]() ,1)
,1)
B.(1,4)
C.(1,8)
D.(8,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在Rt△AOB中,AO=1,BO=2,如圖,動點P是在以O點為圓心,OB為半徑的扇形內運動(含邊界)且∠BOC=90°;設 ![]() ,則x+y的取值范圍 .
,則x+y的取值范圍 . 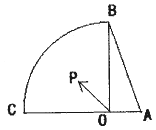
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,{bn}是等比數列,且b2=3,b3=9,a1=b1 , a14=b4 .
(1)求{an}的通項公式;
(2)設cn=an+bn , 求數列{cn}的前n項和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com