
【題目】如圖,在三棱臺(tái)![]() 中,二面角
中,二面角![]() 是直二面角,
是直二面角,![]() ,
,![]() ,
,![]() .
.
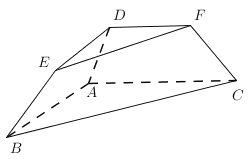
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)見解析;(2)![]()
【解析】分析:(1)由勾股定理可得![]() ,由面面垂直的性質(zhì)可得
,由面面垂直的性質(zhì)可得![]() 平面
平面![]() ,從而可得
,從而可得![]() ,結(jié)合
,結(jié)合![]() ,由線面垂直的判定定理可得
,由線面垂直的判定定理可得![]() 平面
平面![]() ;(2)在平面
;(2)在平面![]() 內(nèi),過點(diǎn)
內(nèi),過點(diǎn)![]() 作
作![]() ,由(1)可知
,由(1)可知![]() ,以
,以![]() 為原點(diǎn),
為原點(diǎn),![]() ,
,![]() ,
,![]() 的方向?yàn)?/span>
的方向?yàn)?/span>![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向,建立空間直角坐標(biāo)系,
軸的正方向,建立空間直角坐標(biāo)系,![]() 是平面
是平面![]() 的一個(gè)法向量,利用向量垂直數(shù)量積為零列方程求出平面
的一個(gè)法向量,利用向量垂直數(shù)量積為零列方程求出平面![]() 的一個(gè)法向量,利用空間向量夾角余弦公式可得結(jié)果.
的一個(gè)法向量,利用空間向量夾角余弦公式可得結(jié)果.
詳解:(1)連接![]() ,在等腰梯形
,在等腰梯形![]() 中,過
中,過![]() 作
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() ,又二面角
,又二面角![]() 是直二面角,
是直二面角,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,又因?yàn)?/span>
,又因?yàn)?/span>![]() ,
,![]() ,
,![]() 、
、![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.

(2)如圖,在平面![]() 內(nèi),過點(diǎn)
內(nèi),過點(diǎn)![]() 作
作![]() ,由(1)可知
,由(1)可知![]() ,以
,以![]() 為原點(diǎn),
為原點(diǎn),![]() ,
,![]() ,
,![]() 的方向?yàn)?/span>
的方向?yàn)?/span>![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向,建立空間直角坐標(biāo)系
軸的正方向,建立空間直角坐標(biāo)系![]() .
.
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,設(shè)
,設(shè)![]() 是平面
是平面![]() 的一個(gè)法向量,則
的一個(gè)法向量,則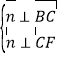 ,所以
,所以![]() ,
,
取![]() ,則
,則![]() ,
,![]() ,
,
即![]() ,
,
由(1)可知![]() 平面
平面![]() ,
,
所以![]() 是平面
是平面![]() 的一個(gè)法向量,
的一個(gè)法向量,
所以
![]() ,
,
又二面角![]() 的平面角為銳角,
的平面角為銳角,
所以二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)a﹤0時(shí),證明![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系
軸的正半軸為極軸建立極坐標(biāo)系![]() ,點(diǎn)A為曲線
,點(diǎn)A為曲線![]() 上的動(dòng)點(diǎn),點(diǎn)B在線段OA的延長線上,且滿足
上的動(dòng)點(diǎn),點(diǎn)B在線段OA的延長線上,且滿足![]() ,點(diǎn)B的軌跡為
,點(diǎn)B的軌跡為![]() .
.
(1)求![]() ,
,![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)設(shè)點(diǎn)C的極坐標(biāo)為(2,0),求△ABC面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知偶函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,且滿
上單調(diào)遞增,且滿![]() ,給出下列判斷:
,給出下列判斷:
①![]() ;②
;②![]() 在
在![]() 上是減函數(shù);③
上是減函數(shù);③![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱;
對稱;
④函數(shù)![]() 在
在![]() 處取得最大值;⑤函數(shù)
處取得最大值;⑤函數(shù)![]() 沒有最小值
沒有最小值
其中判斷正確的序號_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 上的點(diǎn)均在曲線
上的點(diǎn)均在曲線![]() 外,且對
外,且對![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() ,
,![]() 到直線
到直線![]() 的距離等于該點(diǎn)與曲線
的距離等于該點(diǎn)與曲線![]() 上點(diǎn)的距離的最小值.
上點(diǎn)的距離的最小值.
(1)求動(dòng)點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點(diǎn)![]() 的直線與曲線
的直線與曲線![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)![]() 、
、![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線與曲線
的直線與曲線![]() 交于另一點(diǎn)
交于另一點(diǎn)![]() ,且直線
,且直線![]() 過點(diǎn)
過點(diǎn)![]() ,求證:直線
,求證:直線![]() 過定點(diǎn).
過定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)的定義域是(0,+∞),且對任意正實(shí)數(shù)x,y都有f(xy)=f(x)+f(y)恒成立,已知f(2)=1,且x>1時(shí),f(x)>0.
(1)求f(![]() )的值;
)的值;
(2)判斷y=f(x)在(0,+∞)上的單調(diào)性并給出證明;
(3)解不等式f(2x)>f(8x-6)-1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近期,某公交公司分別推出支付寶和微信掃碼支付乘車活動(dòng),活動(dòng)設(shè)置了一段時(shí)間的推廣期,由于推廣期內(nèi)優(yōu)惠力度較大,吸引越來越多的人開始使用掃碼支付,某線路公交車隊(duì)統(tǒng)計(jì)了活動(dòng)剛推出一周內(nèi)每一天使用掃碼支付的人次,用x表示活動(dòng)推出的天數(shù),y表示每天使用掃碼支付的人次(單位:十人次),繪制了如圖所示的散點(diǎn)圖:
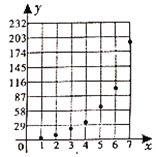
(I)根據(jù)散點(diǎn)圖判斷在推廣期內(nèi),![]() 與
與![]() (c,d為為大于零的常數(shù))哪一個(gè)適宜作為掃碼支付的人次y關(guān)于活動(dòng)推出天數(shù)x的回歸方程類型?(給出判斷即可,不必說明理由)
(c,d為為大于零的常數(shù))哪一個(gè)適宜作為掃碼支付的人次y關(guān)于活動(dòng)推出天數(shù)x的回歸方程類型?(給出判斷即可,不必說明理由)
(Ⅱ)根據(jù)(I)的判斷結(jié)果求y關(guān)于x的回歸方程,并預(yù)測活動(dòng)推出第8天使用掃碼支付的人次.
參考數(shù)據(jù):
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計(jì)分別為:
的斜率和截距的最小二乘估計(jì)分別為: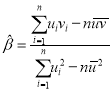 ,
,![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解學(xué)生喜歡校內(nèi)、校外開展活動(dòng)的情況,某中學(xué)一課外活動(dòng)小組在學(xué)校高一年級進(jìn)行了問卷調(diào)查,問卷共100道題,每題1分,總分100分,該課外活動(dòng)小組隨機(jī)抽取了200名學(xué)生的問卷成績(單位:分)進(jìn)行統(tǒng)計(jì),將數(shù)據(jù)按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五組,繪制的頻率分布直方圖如圖所示,若將不低于60分的稱為
分成五組,繪制的頻率分布直方圖如圖所示,若將不低于60分的稱為![]() 類學(xué)生,低于60分的稱為
類學(xué)生,低于60分的稱為![]() 類學(xué)生.
類學(xué)生.

(1)根據(jù)已知條件完成下面![]() 列聯(lián)表,能否在犯錯(cuò)誤的概率不超過
列聯(lián)表,能否在犯錯(cuò)誤的概率不超過![]() 的前提下認(rèn)為性別與是否為
的前提下認(rèn)為性別與是否為![]() 類學(xué)生有關(guān)系?
類學(xué)生有關(guān)系?
|
| 合計(jì) | |
男 | 110 | ||
女 | 50 | ||
合計(jì) |
(2)將頻率視為概率,現(xiàn)在從該校高一學(xué)生中用隨機(jī)抽樣的方法每次抽取1人,共抽取3次,記被抽取的3人中![]() 類學(xué)生的人數(shù)為
類學(xué)生的人數(shù)為![]() ,若每次抽取的結(jié)果是相互獨(dú)立的,求
,若每次抽取的結(jié)果是相互獨(dú)立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
參考公式:![]() ,其中
,其中![]() .
.
參考臨界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com