
【題目】某工廠生產的10件產品中,有8件合格品、2件不合格品,合格品與不合格品在外觀上沒有區別.從這10件產品中任意抽檢2件,計算:
(1)抽出的2件產品恰好都是合格品的抽法有多少種?
(2)抽出的2件產品至多有1件不合格品的抽法有多少種?
(3)如果抽檢的2件產品都是不合格品,那么這批產品將被退貨,求這批產品被退貨的概率.
【答案】(1)28種;(2)44種;(3)![]()
【解析】
(1)根據題意,利用組合數的公式,即可求得抽出的2件都是合格品的抽法種數;
(2)由(1)得抽出的2件產品都是合格品的抽法,再求得恰好1件合格品1件不合格品的抽法種數,利用分類計數原理,即可求解.
(3)求得基本事件的總數,得出其中抽檢的2件產品都是不合格品的事件數,結合古典概型的概率計算公式,即可求解.
(1)由題意,某工廠生產的10件產品中,有8件合格品、2件不合格品,
所以抽出的2件都是合格品的抽法,共有![]() 種.
種.
(2)由(1)得抽出的2件產品都是合格品的抽法,共有![]() 種;
種;
恰好1件合格品1件不合格品的抽法,共有![]() 種,
種,
所以抽到的2件產品中至多有1件不合格品的抽法,共有![]() 種.
種.
(3)從10件產品中任意抽取2件產品的抽法,共有![]() 種,
種,
其中抽檢的2件產品都是不合格品的事件數有![]() 種,
種,
得抽檢的2件產品都是不合格品的概率![]() ,
,
即這批產品被退貨的概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】某城市![]() 戶居民的月平均用電量(單位:度),以
戶居民的月平均用電量(單位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.

(1)求直方圖中![]() 的值;
的值;
(2)求月平均用電量的眾數和中位數;
(3)在月平均用電量為![]() ,
,![]() ,
,![]() ,
,![]() 的四組用戶中,用分層抽樣的方法抽取
的四組用戶中,用分層抽樣的方法抽取![]() 戶居民,則月平均用電量在
戶居民,則月平均用電量在![]() 的用戶中應抽取多少戶?
的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】獨立性檢驗中,假設![]() :運動員受傷與不做熱身運動沒有關系.在上述假設成立的情況下,計算得
:運動員受傷與不做熱身運動沒有關系.在上述假設成立的情況下,計算得![]() 的觀測值
的觀測值![]() .下列結論正確的是( )
.下列結論正確的是( )
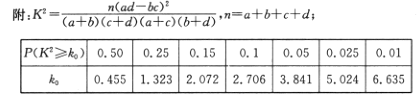
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯錯誤的概率不超過0.01的前提下,認為運動員受傷與不做熱身運動有關
B. 在犯錯誤的概率不超過0.01的前提下,認為運動員受傷與不做熱身運動無關
C. 在犯錯誤的概率不超過0.005的前提下,認為運動員受傷與不做熱身運動有關
D. 在犯錯誤的概率不超過0.005的前提下,認為運動員受傷與不做熱身運動無關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網購是當前民眾購物的新方式,某公司為改進營銷方式,隨機調査了100名市民,統計其周平均網購
的次數,并整理得到如右的頻數直方圖,將周平均網購次數不小于4次的民眾稱為網購迷.這100名市民中,年齡不超過40歲的有65人,且網購迷中有5名市民的年齡超過40歲
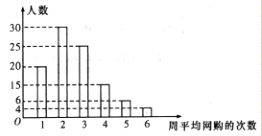
(1)根據已知條件完成下面的2×2列聯表,能否在犯錯誤的概率不超過0.10的前提條件下認為網購迷與年齡不超過40歲有關?

(2)現從網購迷中按分層抽樣選5人代表進一步進行調查,若從5人代表中任意挑選2人,求挑選的2人中有年齡超過40歲的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,短軸長為
,短軸長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,
兩點,![]() 是橢圓
是橢圓![]() 的上焦點.問:是否存在直線
的上焦點.問:是否存在直線![]() ,使得
,使得![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一工廠生產了某種產品700件,該工廠需要對這些產品的性能進行檢測現決定利用隨機數表法從中抽取100件產品進行抽樣檢測,將700件產品按001,002,…,700進行編號
(1)如果從第8行第4列的數開始向右讀,請你依次寫出最先檢測的3件產品的編號;(下面摘取了隨機數表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)檢測結果分為優等、合格、不合格三個等級,抽取的100件產品的安全性能和環保性能的檢測結果如下表(橫向和縱向分別表示安全性能和環保性能):
(i)若在該樣本中,產品環保性能是優等的概率為34%,求![]() 的值;
的值;
(ii)若![]() ,求在安全性能不合格的產品中,環保性能為優等的件數比不合格的件數少的概率.
,求在安全性能不合格的產品中,環保性能為優等的件數比不合格的件數少的概率.
件數 | 環保性能 | |||
優等 | 合格 | 不合格 | ||
安全性能 | 優等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 | m | 4 | n | |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,且函數
,且函數![]() 是偶函數.
是偶函數.
(1)求![]() 的解析式;.
的解析式;.
(2)若不等式![]() 在
在![]() 上恒成立,求n的取值范圍;
上恒成立,求n的取值范圍;
(3)若函數 恰好有三個零點,求k的值及該函數的零點.
恰好有三個零點,求k的值及該函數的零點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com