
���}Ŀ����֪�Aб��60����ֱ��lƽ�ֈA��x2+y2+2x+4y��4=0���tֱ��l�ķ��̞飨 ��
A.![]() x��y+
x��y+ ![]() +2=0
+2=0
B.![]() x+y+
x+y+ ![]() +2=0
+2=0
C.![]() x��y+
x��y+ ![]() ��2=0
��2=0
D.![]() x��y��
x��y�� ![]() +2=0
+2=0
���𰸡�C
���������⣺�Aб��60���ֱ�����̣��O(sh��)��y= ![]() x+b��
x+b��
�A��x2+y2+2x+4y��4=0���飨x+1��2+��y+2��2=9���A������(bi��o)����1����2����
��?y��n)�ֱ��ƽ�ֈA���A����ֱ��y= ![]() x+b�ϣ����ԩ�2=��
x+b�ϣ����ԩ�2=�� ![]() +b�����b=
+b�����b= ![]() ��2��
��2��
������ֱ�����̞� ![]() x��y+
x��y+ ![]() ��2=0��
��2=0��
���xC��
�����c(di��n)����������ֱ���c�A�����Nλ���P(gu��n)ϵ�ǽ���}�ĸ�������Ҫ֪��ֱ���c�A�����Nλ���P(gu��n)ϵ���o�����c(di��n)�����x���Ѓɂ������c(di��n)���ཻ,�@�lֱ�������A�ĸ���A�cֱ����Ψһ�����c(di��n)�����У��@�lֱ�������A���о����@��Ψһ�Ĺ����c(di��n)�������c(di��n)��


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����x��R�ϵĺ���(sh��)f��x��������0��x2��x1���� ![]() ��1���Һ���(sh��)y=f��x���ĈD���P(gu��n)��ԭ�c(di��n)���Q����f��2��=2���t����ʽf��x����x��0�Ľ⼯�ǣ� ��
��1���Һ���(sh��)y=f��x���ĈD���P(gu��n)��ԭ�c(di��n)���Q����f��2��=2���t����ʽf��x����x��0�Ľ⼯�ǣ� ��
A.����2��0���ȣ�0��2��
B.�����ޣ���2���ȣ�2��+�ޣ�
C.�����ޣ���2���ȣ�0��2��
D.����2��0���ȣ�2��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��) ![]() ���ҝM��cosa=a��sin��cosb��=b��cos��sinc��=c���ta��b��c�Ĵ�С�P(gu��n)ϵ�� ��
���ҝM��cosa=a��sin��cosb��=b��cos��sinc��=c���ta��b��c�Ĵ�С�P(gu��n)ϵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���(xi��ng)��������(sh��)�Ĕ�(sh��)��{an}��ǰn�(xi��ng)�͞�Sn �� �M��a ![]() =2Sn+n+4����a2��1��a3 �� a7ǡ��ȱȔ�(sh��)��{bn}��ǰ3�(xi��ng)��
=2Sn+n+4����a2��1��a3 �� a7ǡ��ȱȔ�(sh��)��{bn}��ǰ3�(xi��ng)��
��1����(sh��)��{an}��{bn}��ͨ�(xi��ng)��ʽ��
��2����cn= ![]() ��
�� ![]() ����(sh��)��{cn}��ǰn�(xi��ng)��Tn ��
����(sh��)��{cn}��ǰn�(xi��ng)��Tn ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪a�鳣��(sh��)������(sh��)f��x��=xlnx�� ![]() ax2 ��
ax2 ��
��1����(d��ng)a=0�r(sh��)����(sh��)f��x������Сֵ��
��2����f��x���Ѓɂ��Oֵ�c(di��n)x1 �� x2��x1��x2��
����(sh��)��(sh��)a��ȡֵ������
�����C��x1x2��1��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(zh��)����D��ʾ�ij����D���tݔ���Y(ji��)��s��ֵ�飨 �� 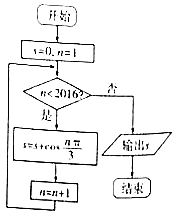
A.�� ![]()
B.��1
C.![]()
D.0
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AC�� ![]() =1��a��b��0��������c(di��n)�飨0��2�������x���ʞ�
=1��a��b��0��������c(di��n)�飨0��2�������x���ʞ� ![]() �� ������E�AC�ķ��̣�
�� ������E�AC�ķ��̣�
���ęE�AC��һ�c(di��n)M��Ax2+y2=1�����ɗl�о������c(di��n)�քe��A��B����(d��ng)ֱ��AB�քe�cx�S��y�S����P��Q���c(di��n)�r(sh��)����|PQ|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(zh��)����D�ij����D���tݔ��S��ֵ�飨 �� 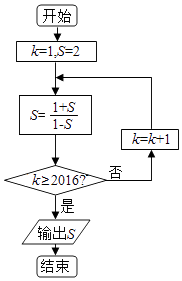
A.2
B.��3
C.�� ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)��(sh��)��(sh��)a��R������(sh��) ![]() ��R�ϵ��溯��(sh��)�� ������(sh��)��(sh��)a��ֵ��
��R�ϵ��溯��(sh��)�� ������(sh��)��(sh��)a��ֵ��
����(d��ng)x�ʣ�1��1���r(sh��)����M�㲻��ʽf��1m��+f��1m2����0�Č�(sh��)��(sh��)m��ȡֵ������
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com