
���}Ŀ����֪���タ![]() ����c(di��n)��ԭ�c(di��n)���佹�c(di��n)
����c(di��n)��ԭ�c(di��n)���佹�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ���O(sh��)
���O(sh��)![]() ��ֱ��
��ֱ��![]() �ϵ��c(di��n)���^�c(di��n)
�ϵ��c(di��n)���^�c(di��n)![]() �����タ
�����タ![]() �ăɗl�о�
�ăɗl�о�![]() ������
������![]() �����c(di��n)��
�����c(di��n)��
(1) ���タ![]() �ķ��̣�
�ķ��̣�
(2) ��(d��ng)�c(di��n)![]() ��ֱ��
��ֱ��![]() �ϵĶ��c(di��n)�r(sh��)����ֱ��
�ϵĶ��c(di��n)�r(sh��)����ֱ��![]() �ķ��̣�
�ķ��̣�
(3) ��(d��ng)�c(di��n)![]() ��ֱ��
��ֱ��![]() ���Ƅ�(d��ng)�r(sh��)����
���Ƅ�(d��ng)�r(sh��)����![]() ����Сֵ��
����Сֵ��
���𰸡�(��) ![]() (��)
(��) ![]() (��)
(��) ![]()
��������ԇ�}��������1���O(sh��)���タ![]() �ķ��̞�
�ķ��̞�![]() �������c(di��n)��ֱ���ľ��x,���
�������c(di��n)��ֱ���ľ��x,���![]() ,�õ����タ���̣���2�������タ������(d��o),����о�
,�õ����タ���̣���2�������タ������(d��o),����о�![]() ��б��,���c(di��n)бʽ�����о�����,����һ��ʽ,�ҳ���ͬ�c(di��n),�õ�ֱ��
��б��,���c(di��n)бʽ�����о�����,����һ��ʽ,�ҳ���ͬ�c(di��n),�õ�ֱ��![]() �ķ��̣���3���ɒ��タ���x��֪
�ķ��̣���3���ɒ��タ���x��֪![]() ��(li��n)��ֱ���c���タ����,��ȥ
��(li��n)��ֱ���c���タ����,��ȥ![]() ,�õ�һ��(g��)�P(gu��n)��
,�õ�һ��(g��)�P(gu��n)��![]() ��һԪ���η���,���f�_(d��)�������
��һԪ���η���,���f�_(d��)�������![]() ��ֵ,߀��
��ֵ,߀��![]() ,��
,��![]() ��ʾ��
��ʾ��![]() �Ķ��κ���(sh��)����ʽ,�������ֵ.
�Ķ��κ���(sh��)����ʽ,�������ֵ.
ԇ�}����: �⣺��1�����}�⣬�O(sh��)���タ![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() �Y(ji��)��
�Y(ji��)��![]() ��
��
���![]() �����Ԓ��タ
�����Ԓ��タ![]() �ķ��̞�
�ķ��̞�![]() .
.
��2�����タ![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ����(d��o)��
����(d��o)��![]() ��
��
�O(sh��)![]() (����
(����![]() )�t�о�
)�t�о�![]() ��б�ʷքe��
��б�ʷքe��![]() ��
��
�����о�![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ����
����![]() ��
��
ͬ���ɵ��о�![]() �ķ��̞�
�ķ��̞�![]() ��
��
��?y��n)��о�![]() ���^�c(di��n)
���^�c(di��n)![]() ������
������![]() ��
�� ![]() ��
��
����![]() �鷽��
�鷽��![]() �ăɽM�⣬
�ăɽM�⣬
����ֱ��![]() �ķ��̞�
�ķ��̞�![]() .
.
��3���ɒ��タ���x��֪![]() ��
��
(li��n)������![]() ����ȥ
����ȥ![]() ������
������![]() .
.
��һԪ���η��̸��cϵ��(sh��)���P(gu��n)ϵ�ɵ�![]() ��
��
����![]()
���c(di��n)![]() ��ֱ��
��ֱ��![]() �ϣ�����
�ϣ�����![]() ��
��
����![]() ��
��
���Ԯ�(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ȡ����Сֵ,��ȡ����Сֵ��
ȡ����Сֵ,��ȡ����Сֵ��![]() .
.


 ���ˈD���옷����������I(y��)���ݴ�W(xu��)������ϵ�д�
���ˈD���옷����������I(y��)���ݴ�W(xu��)������ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
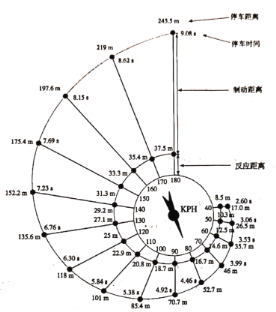
���}Ŀ����܇���x܇��ͣ܇���x�c�T���������P(gu��n),��������P(gu��n)�I�ăɂ�(g��)�������{�T�ķ���(y��ng)�r(sh��)�g����܇�����ٶ�.�O(sh��)d��ʾͣ܇���x,![]() ��ʾ����(y��ng)���x,
��ʾ����(y��ng)���x,![]() ��ʾ�Ƅ�(d��ng)���x,�t
��ʾ�Ƅ�(d��ng)���x,�t![]() .�D�Ǹ���(j��)������·�ֹ�����ԇ�(y��n)��(sh��)��(j��)������ͣ܇���xʾ��D������(y��ng)����܇�����ٶ��cͣ܇���x�ı������D��ʾ
.�D�Ǹ���(j��)������·�ֹ�����ԇ�(y��n)��(sh��)��(j��)������ͣ܇���xʾ��D������(y��ng)����܇�����ٶ��cͣ܇���x�ı������D��ʾ
��̖ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��1������(j��)�����еĔ�(sh��)��(j��),����ͣ܇���x�c��܇�ٶȵĺ���(sh��)ģ��.���x��ģ��һ:![]() ��ģ�Ͷ�:
��ģ�Ͷ�:![]() ������v����܇�ٶ�,a,b
������v����܇�ٶ�,a,b
��2��ͨ�^Ӌ(j��)��![]() �r(sh��)��ͣ܇���x,�����x����һ��(g��)����(sh��)ģ�͵ĔM��Ч������.
�r(sh��)��ͣ܇���x,�����x����һ��(g��)����(sh��)ģ�͵ĔM��Ч������.
��������(sh��)��(j��):![]() ;
;![]() ;
;![]() .��
.��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��(��С�}�M��10��)һλ�W(w��ng)���ھW(w��ng)�Ϲ��ij�Ԍ�С�꣬��(j��ng)�^һ���g�[��ԓ����е�![]() ��N��Ʒ��ُ�I����.��֪ԓ�W(w��ng)��ُ�I
��N��Ʒ��ُ�I����.��֪ԓ�W(w��ng)��ُ�I![]() �ɷN��Ʒ�ĸ��ʾ���
�ɷN��Ʒ�ĸ��ʾ���![]() ��ُ�I
��ُ�I![]() �ɷN��Ʒ�ĸ��ʾ���
�ɷN��Ʒ�ĸ��ʾ���![]() ��ُ�I
��ُ�I![]() �N��Ʒ�ĸ��ʞ�
�N��Ʒ�ĸ��ʞ�![]() .���O(sh��)ԓ�W(w��ng)���Ƿ�ُ�I�@��N��Ʒ���(d��)��.
.���O(sh��)ԓ�W(w��ng)���Ƿ�ُ�I�@��N��Ʒ���(d��)��.
��1����ԓ�W(w��ng)������ُ�I4�N��Ʒ�ĸ��ʣ�
��2�����S�C(j��)׃��![]() ��ʾԓ�W(w��ng)��ُ�I��Ʒ�ķN��(sh��)����
��ʾԓ�W(w��ng)��ُ�I��Ʒ�ķN��(sh��)����![]() �ĸ��ʷֲ��͔�(sh��)�W(xu��)����.
�ĸ��ʷֲ��͔�(sh��)�W(xu��)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() �������څ^(q��)�g
�������څ^(q��)�g![]() ��ʹ��
��ʹ��![]() ��
��![]() �ϵ�ֵ��?y��n)?/span>
�ϵ�ֵ��?y��n)?/span>![]() ���t
���t![]() ��ȡֵ�����ǣ� ��
��ȡֵ�����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���՚��|(zh��)��ָ��(sh��)AQI�Ƿ�ӳ�՚��|(zh��)����r��ָ��(sh��)��AQIָ��(sh��)ֵԽС�������՚��|(zh��)��Խ�ã��䌦��(y��ng)�P(gu��n)ϵ���±���
AQIָ��(sh��)ֵ | 0��50 | 51��100 | 101��150 | 151��200 | 201��300 | ��300 |
�՚��|(zh��)�� | ��(y��u) | �� | �p����Ⱦ | �ж���Ⱦ | �ض���Ⱦ | ��(y��n)����Ⱦ |
�D��ij��10��1�ա�20��AQIָ��(sh��)׃��څ�ݣ�

�������e(cu��)�`����
A. �@20����AQIָ��(sh��)ֵ����λ��(sh��)�Ը���100
B. �@20���е��ж���Ⱦ�����ϵ��씵(sh��)ռ![]()
C. ԓ��10�µ�ǰ�낀(g��)�µĿ՚��|(zh��)��Խ��Խ��
D. ���w���f��ԓ��10����Ѯ�Ŀ՚��|(zh��)������Ѯ�Ŀ՚��|(zh��)����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
(1)ӑՓ����(sh��)![]() �Ķ��x��
�Ķ��x��
(2)��(d��ng)![]() �r(sh��)�����P(gu��n)��x�IJ���ʽ��
�r(sh��)�����P(gu��n)��x�IJ���ʽ��![]()
(3)��(d��ng)![]() �r(sh��)������ʽ
�r(sh��)������ʽ![]() �����⌍(sh��)��(sh��)
�����⌍(sh��)��(sh��)![]() ���������(sh��)��(sh��)m��ȡֵ����.
���������(sh��)��(sh��)m��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
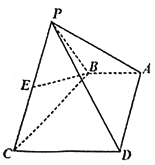
���}Ŀ����D�������F![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n).
���c(di��n).
��1���C����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ƽ��
ƽ��![]() ��
��![]() ��߅�L��2���������Σ����c(di��n)
��߅�L��2���������Σ����c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x.
�ľ��x.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ż����(sh��)![]() ���x��?y��n)?/span>
���x��?y��n)?/span>![]() ���䌧(d��o)����(sh��)��
���䌧(d��o)����(sh��)��![]() ����(d��ng)
����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ���t�P(gu��n)��
���t�P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯�飨 ��
�Ľ⼯�飨 ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�A![]() ��һ��(d��ng)�c(di��n)
��һ��(d��ng)�c(di��n)![]() ���^�c(di��n)
���^�c(di��n)![]() ��
��![]() �S�������
�S�������![]() �c(di��n)��
�c(di��n)��![]() ���c(di��n)��
���c(di��n)��![]() ��
��
��1����(d��ng)![]() �ڈA
�ڈA![]() ���\(y��n)��(d��ng)�r(sh��)�����c(di��n)
���\(y��n)��(d��ng)�r(sh��)�����c(di��n)![]() ��܉�E
��܉�E![]() �ķ�����
�ķ�����
�����^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c
�c![]() ����
����![]() ���c(di��n)����(d��ng)
���c(di��n)����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �Ĵ�ֱƽ�־����̣�
�Ĵ�ֱƽ�־����̣�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com